---

figsize(12.5, 4)
 
import scipy.stats as stats
binomial = stats.binom
 
parameters = [(10, .4), (10, .9)]
colors = [”#348ABD”, ”#A60628”]
 
for i in range(2):
    N, p = parameters[i]
    _x = np.arange(N + 1)
    plt.bar(_x - 0.5, binomial.pmf(_x, N, p), color=colors[i], edgecolor=colors[i], alpha=0.6,label=”$N$: %d, $p$: %.1f“ % (N, p), linewidth=3)
 
plt.legend(loc=“upper left”)
plt.xlim(0, 10.5)
plt.xlabel(”$k$”)
plt.ylabel(”$P(X = k)$”)
plt.title(“이항확률변수의 확률질량분포”)

---

 

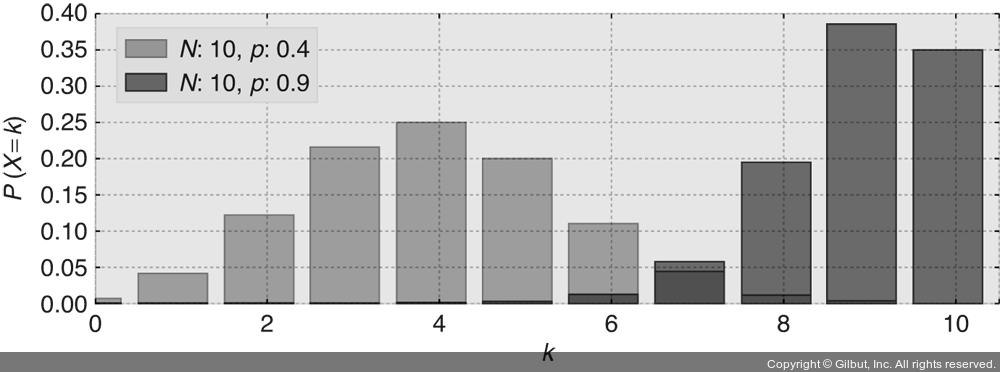
▲ 그림 2-8 이항확률변수의 확률질량분포

 

N = 1일 때 이항분포는 베르누이분포가 되는 특별한 경우이다. 베르누이분포와 이항확률변수 간에는 또 다른 연결고리가 있다. 만일 동일한 모수 p를 가진 베르누이 확률변수 X₁, X₂, …, X_N이 있다면 Z = X₁ + X₂ + … + X_N은 모수가 N과 p인 이항분포를 따르게 된다.