---

figsize(12.5, 3)
p_trace = mcmc.trace(“freq_cheating”)[:]
plt.hist(p_trace, histtype=“stepfilled”, normed=True, alpha=0.85, bins=30,label=“사후확률분포”, color=”#348ABD”)
plt.vlines([.05, .35], [0, 0], [5, 5], alpha=0.3)
plt.xlim(0, 1)
plt.xlabel(”$p$의 값”)
plt.ylabel(“밀도”)
plt.ylabel(“모수 $p$의 사후확률분포”)
plt.legend();

---

 

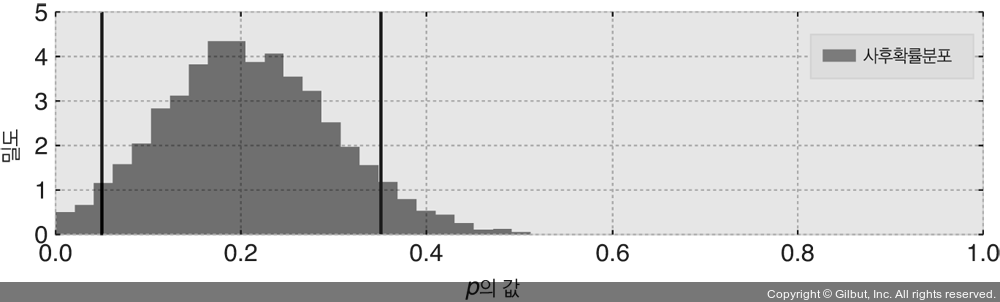
▲ 그림 2-9 모수 p의 사후확률분포

 

우리는 부정행위자의 실제 빈도가 무엇인지 여전히 확신하지 못하지만, 그림 2-9를 보면 0.05~0.35 사이로(실선으로 표시) 범위를 좁혔다. 사전확률로 상당히 괜찮은데, 사전에 얼마나 많은 학생이 부정행위를 했는지 몰랐기 때문이다(그래서 사전확률분포로 균등분포를 선택한 것이다). 반면에 상당히 나쁘기도 한데, ‘0.3’이라는 범위 내에 참 값이 존재할 가능성이 있기 때문이다. 심지어 우리는 무엇을 얻었는가? 여전히 진짜 빈도에 대해서 확신하지 못하는가?

나는 우리가 무언가를 발견했다고 주장하겠다. 우리의 사후확률에 따르면 부정행위자가 없다. 즉, 사후확률은 p = 0에 낮은 확률을 부여하는데, 이는 믿기 어렵다. 균등 사전확률로 시작한 이후 p의 모든 값을 동일하게 타당한 값으로 취급하고 있지만, 데이터는 잠재적으로 p = 0을 배제하므로 부정행위자가 있었다고 확신할 수 있다.

이런 종류의 알고리즘은 사용자의 개인정보를 수집하는 데 사용될 수 있고, 비록 노이즈가 있더라도 데이터가 진실하다는 것을 합리적으로 확신할 수 있다.