2 지수함수의 평행 이동과 대칭 이동
지수함수의 평행 이동
지수함수 y = ax을 평행 이동하면 어떻게 표현할 수 있을까요? 평행 이동이기 때문에 그래프 모양은 바뀌지 않으면서 위치만 바뀔 것입니다. 즉, 원래의 점 f(x, y) = 0을 (p, q)만큼 이동한다고 하면 f(x - p, y - q) = 0이 됩니다.
이를 정리하면 다음과 같습니다.
그림 6-4의 ①과 같이 y = ax에서 원래의 점 f(x, y) = 0에 대해 평행 이동한다고 가정해 봅시다.
②와 같이 x축 방향으로 p만큼 평행 이동한다면 x 대신 x - p를 대입하여 f(x - p, y) = 0이 되고,
③과 같이 y축 방향으로 q만큼 평행 이동한다면 y 대신 y - q를 대입하여 f(x, y - q) = 0이 됩니다.
또 ④와 같이 x축으로 p만큼, y축으로 q만큼 평행 이동한다면 f(x - p, y - q) = 0이 됩니다.
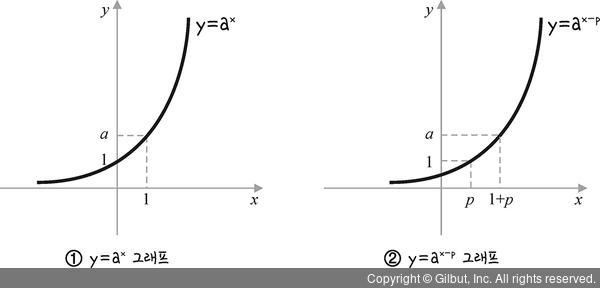
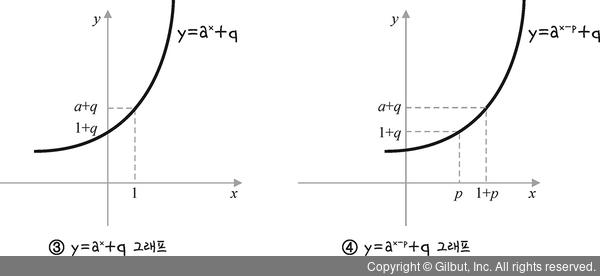
그림 6-4 | 지수함수의 평행 이동
지수함수의 대칭 이동
지수함수 y = ax의 대칭 이동은 어떨까요? x축, y축 및 원점을 기준으로 대칭 이동했을 때를 알아봅시다. 지수함수 y = ax 그래프를 x축에 대칭 이동하면 -y = ax이 되어 y = -ax이 됩니다. 또 y축에 대칭 이동하면 y = a-x이 되고, 원점에 대칭 이동하면 -y = a-x이 됩니다.
이를 정리하면 다음과 같습니다.
그림 6-5의 ①과 같이 y = ax에서 원래의 점 f(x, y) = 0에 대해 대칭 이동한다고 가정해 봅시다.
②와 같이 y축에 대해 대칭 이동한다면 x 대신 -x를 대입하여 f(-x, y) = 0이 되고,
③과 같이 x축에 대해 대칭 이동한다면 y 대신 -y를 대입하여 f(x, -y) = 0이 됩니다.
또 ④와 같이 원점에 대해 대칭 이동한다면 x 대신 -x를, y 대신 -y를 대입하여 f(-x, -y) = 0이 됩니다.
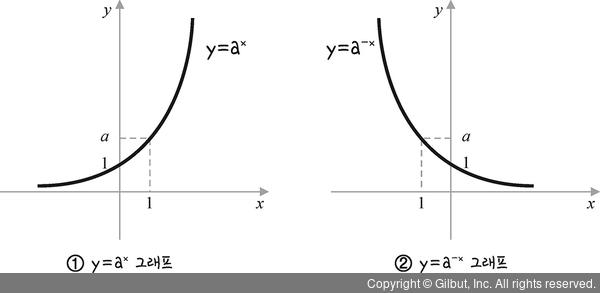
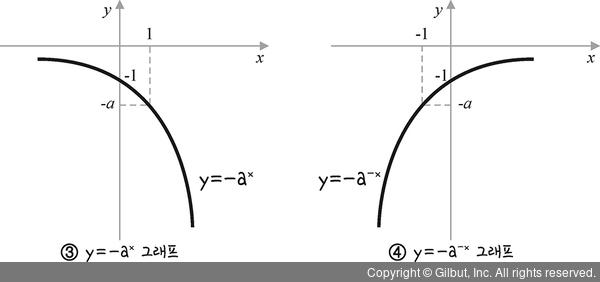
그림 6-5 | 지수함수의 대칭 이동
즉, 지수함수의 그래프는 x축과 만나지 않으며, 반드시 y축을 지나고 그 점은 1 또는 -1입니다.
연습 문제
(1) y = 2x 그래프를 이용하여 함수 y = 2x-3 그래프를 그리세요.
(2) y = 2x-3 그래프를 이용하여 y = -2x-3 그래프를 그리세요.
문제 풀이
(1) y = 2x-3 그래프는 지수함수 y = 2x 그래프에서 x축 방향으로 3만큼 평행 이동한 것입니다. 따라서 y = 2x-3 그래프는 다음과 같습니다.
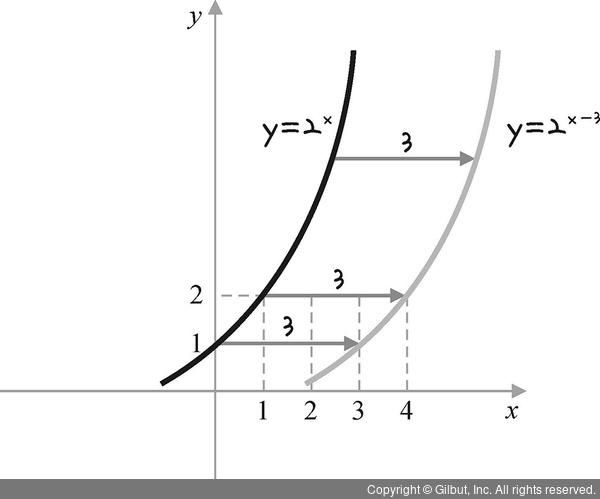
그림 6-6 | y = 2x-3 그래프
(2) y = -2x-3 그래프는 지수함수 y = 2x-3 그래프에서 x축으로 대칭 이동한 것입니다. 따라서 y = -2x-3 그래프는 다음과 같습니다.
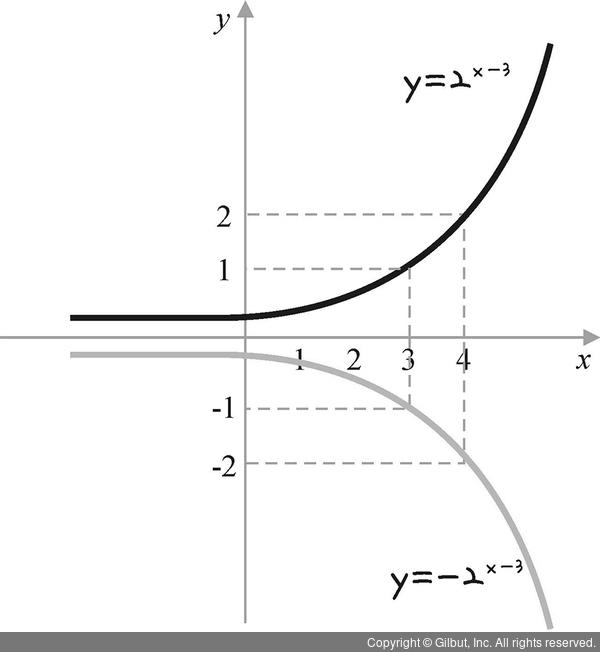
그림 6-7 | y = -2x-3 그래프
잠 깐 만 요
로지스틱 함수란
로지스틱(logistic) 함수는 지수함수를 변형한 것으로, 회귀분석이나 인공신경망에서 자주 사용합니다. 로지스틱 회귀는 분석 결과가 범주형일 때 사용하는 방식입니다. 예를 들어 수학 시험 결과에 따른 그룹이 표 6-4와 같다고 합시다.
|
점수 |
91~100점 |
81~90점 |
71~80점 |
70점 이하 |
|
그룹 |
A |
B |
C |
D |
표 6-4 | 수학 시험 결과에 따른 학생 그룹
표와 같이 학생들 점수에 따라 자동으로 그룹을 분류하는 형태를 범주형 분석이라고 하며, 로지스틱 회귀를 자주 사용합니다.
로지스틱 회귀는 로지스틱 함수를 사용하여 분석합니다.
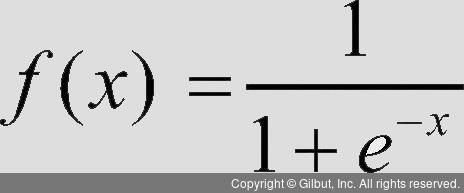
로지스틱 함수를 사용할 때는 다음과 같이 x 값과 무관하게 f(x)는 0과 1 사이의 값을 갖습니다.
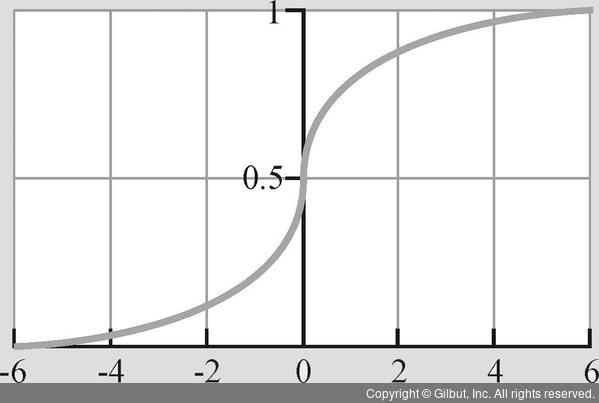
그림 6-8 | 로지스틱