그림 7-2와 같이 f(x) 함수 위에 P(a, f(a))라는 점이 있고, a에서 오른쪽(→)과 위쪽(↑)으로 h만큼 움직인 Q(a + h, f(a + h))라는 두 점이 있을 때, 점 P와 Q 사이의 기울기는 수식 7.1처럼 표현할 수 있습니다.

수식 7.1

기울기 = =

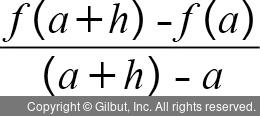
미분은 한 점에서의 기울기라고 정의했습니다. 이때 ‘기울기’ 의미에 주목해야 합니다. 기울기이기는 한데, x의 증가량이 0과 가까워질 때의 기울기입니다. 따라서 수식 7.1에서 x의 증가량이 ((a + h) - a)라고 표현했으므로 a - a + h가 되어, 결국 x의 증가량은 h가 됩니다. h를 0으로 보내면 수식 7.2처럼 표현할 수 있습니다.

수식 7.2

=

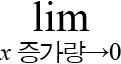
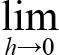
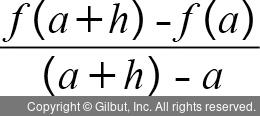
그림 7-2에서 점 Q가 점 P의 0에 가까워진다면, 다음과 같이 기울기가 변하면서 결국 한 점 P에서의 기울기가 됩니다.

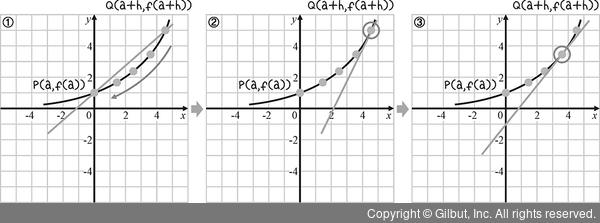
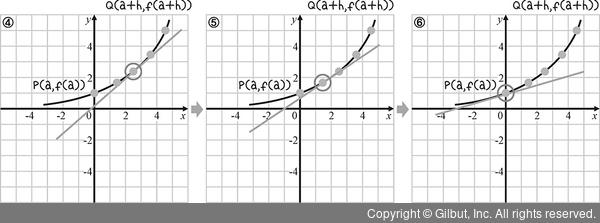
그림 7-3 | x의 증가량을 0으로 보냈을 때 기울기의 변화