여기에서 x → a 의미는 다음과 같습니다.

(1) x와 a가 같지 않다면(x ≠ a) a에 한없이 가까이 가는 상태를 의미합니다.

(2) 좌극한(x → a - 0)과 우극한(x → a + 0) 두 경우를 묶어서 x → a로 나타냅니다.

특히 상수함수 f(x) = c (c는 상수)는 모든 x 값에 대해 항상 같은 값 c를 출력합니다. 따라서 a 값에 관계없이 다음이 성립합니다.

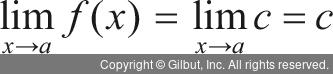
예를 들어 함수 f(x) = 에서 x = 1이면 분모가 0이 되므로 x = 1에서 함수 값 f(1)은 정의되지 않습니다(f(1) 값이 정의되지 않았기에 그림 7-6의 f(1)에서 구멍이 비어 있습니다). 하지만 x ≠ 1일 경우에는 f(x) = = = x + 1이므로 x가 1이 아닌 값을 가지면서 1에 한없이 가까워지면 f(x)는 2에 가까워집니다.

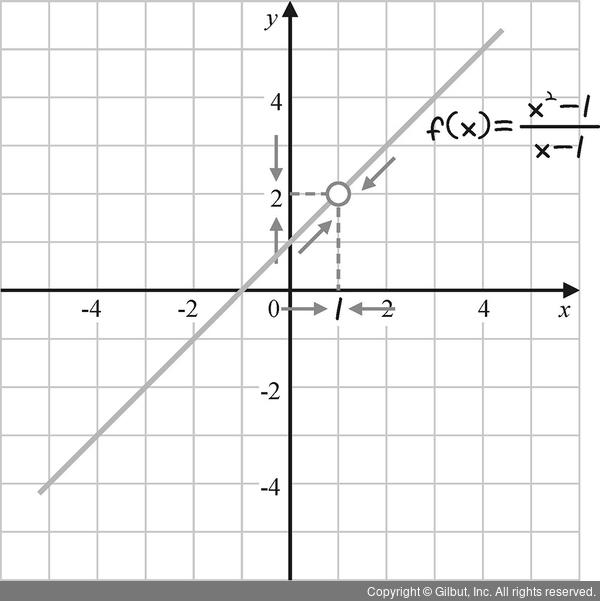
그림 7-6 | 함수 f(x) = 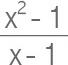의 수렴

연습 문제

x → 2일 때, 함수 f(x) = 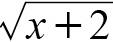의 극한을 구하세요.