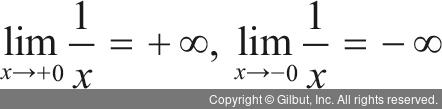함수의 발산

함수의 발산이란 함수 f(x)에서 함수 값이 어떤 실수 값에 수렴하지 않고 무한히 커지는 것을 의미합니다. 함수의 발산에는 양의 무한대 발산과 음의 무한대 발산, 진동이 있습니다.

양의 무한대 발산은 함수 f(x)에서 x 값이 a에 한없이 가까워질때, f(x) 값이 한없이 커지면 f(x)는 양의 무한대로 발산한다 하고 다음과 같이 나타냅니다.

x → a일 때, f(x) → ∞ 또는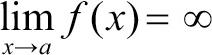

음의 무한대로 발산은 함수 f(x)에서 x 값이 a에 한없이 가까워질때, f(x) 값이 음수이면서 그 절댓값이 한없이 커지면 f(x)는 음의 무한대로 발산한다 하고 다음과 같이 나타냅니다.

x → a일 때, f(x) → -∞ 또는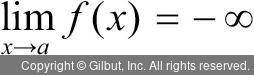

예시에서 확인해 봅시다.

그림 7-9의 ①에서 f(x) = 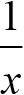그래프는 양의 무한대와 음의 무한대로 확장됩니다. x가 +0으로 한없이 가까워질 때 +∞가 되고, x가 -0으로 한없이 가까워질 때 -∞가 됩니다. 즉, 다음 결과를 도출할 수 있습니다.