그렇다면 함수 값에 대해 범위가 정해져 있다면 어떨까요? {x | a ≤ x ≤ b}일 때 이차함수 y = a(x - p)2 + q의 최댓값과 최솟값을 알아봅시다.
(1) 꼭지점의 x 좌표가 a ≤ x ≤ b에 포함되는 경우
꼭지점의 x 좌표가 a ≤ x ≤ b에 포함되는 경우에는 f(a), f(p), f(b) 값 중 가장 큰 값이 최댓값이고, 가장 작은 값이 최솟값입니다.
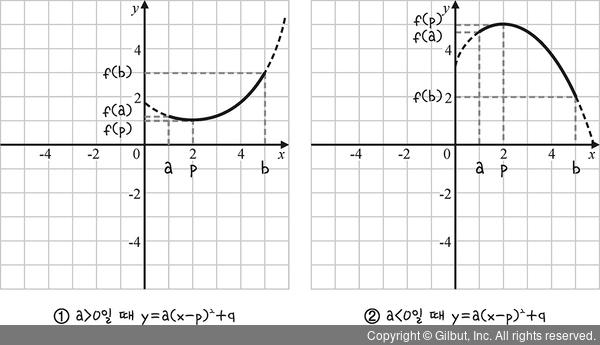
그림 7-21 | 꼭지점의 x 좌표가 a ≤ x ≤ b에 포함될 때
즉, 그림 7-21의 ①과 같이 a > 0일 때 최댓값은 f(b)고, 최솟값은 f(p)입니다. 또 그림 7-21의 ②와 같이 a < 0일 때 최댓값은 f(p)고, 최솟값은 f(b)입니다.