문제 풀이
(1) 이차함수 y = x2 - 2x + 3의 최댓값과 최솟값을 구하세요.
(2) x 값 범위가 {2 ≤ x ≤ 3}인 이차함수 f(x) = x2 - 2x + 3의 최댓값과 최솟값을 구하세요.
문제 풀이
그래프를 이용하여 문제를 풀어 봅시다.
(1) y = x2 - 2x + 3 그래프는 다음과 같습니다.
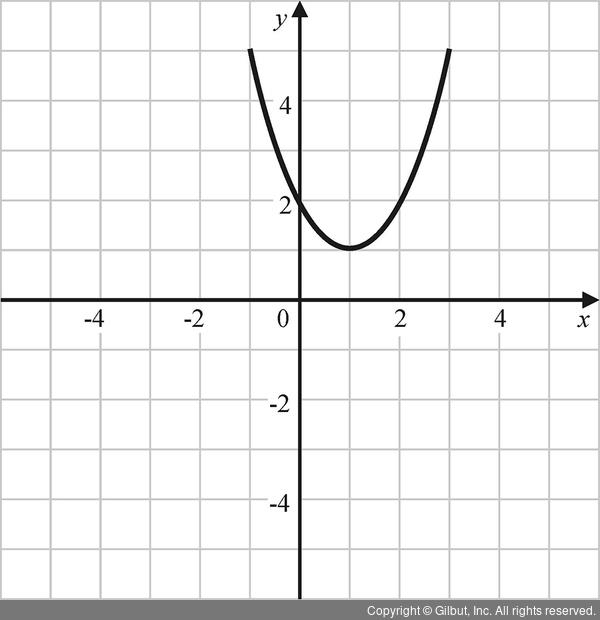
그림 7-23 | y = x2 - 2x + 3
y = x2 - 2x + 3을 인수분해하면 y = (x - 1)2 + 2가 됩니다. 따라서 그림 7-23과 같이 최댓값은 없으며, 최솟값은 1입니다.
(2) f(x) = x2 - 2x + 3을 인수분해하면 f(x) = (x - 1)2 + 2가 됩니다. 또 x 값 범위가 {2 ≤ x ≤ 3}이므로 f(2) = 3, f(3) = 6입니다. 따라서 최댓값은 6, 최솟값은 3입니다.
1 
에서의 수렴: x → ∞ 혹은 x → -∞일 때, f(x) = 
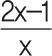처럼 분모와 분자에 x가 있는 형태()에서의 계산은 분모의 최고차항으로 분모와 분자를 나누어 줍니다.