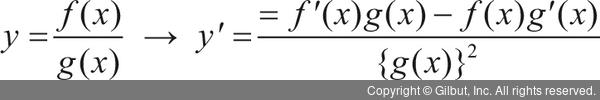(4) {f(x) ± g(x)}' = f '(x) ± g'(x)

즉, 미분할 수 있는 두 함수의 합으로 표현했다면, 각각 따로 미분하여 부호를 연결하면 됩니다. 예를 들어 y = 5x² + 2x를 미분해 봅시다. 먼저 5x²을 미분하면 5x² = 5×2x = 10x가 되고, 2x를 미분하면 2가 됩니다. 따라서 y = 5x² + 2x를 미분하면, y' = 10x + 2가 됩니다.

(5) {f(x)g(x)}' = f '(x)g(x) + f(x)g'(x)

곱으로 표현된 함수의 미분입니다. 좀 더 쉽게 정리하면 수식 8.1과 같습니다.

수식 8.1

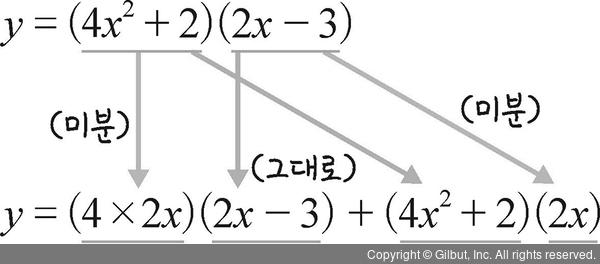
예를 들어 y = (5x + 2)(x² - 3) 함수를 미분하면 다음과 같이 y' = 5(x² - 3) + (5x + 2)2x가 됩니다.

수식 8.2

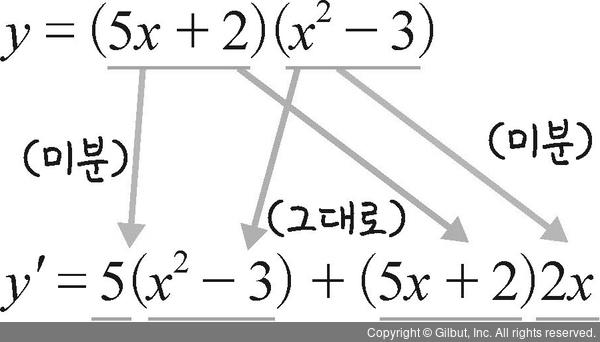
참고로 분수에 대한 미분 공식은 다음과 같습니다.