곱셈의 순전파 역시 순차적으로 계산하면 되기에 어렵지 않지만, 역전파는 미분 방법을 알아야 합니다. 곱셈의 역전파에 대한 미분은 다음과 같습니다.

z = xy

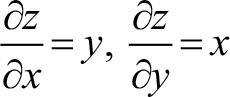
즉, 그림 9-16의 왼쪽과 같은 미분이 가능합니다. 이때 상류에서 1.5 값이 입력되었다고 가정하면 그림 9-16의 오른쪽과 같이 곱셈 노드의 역전파는 상류(출력) 값에 순전파의 입력 신호를 ‘서로 바꾼 값’을 곱해서 하류(은닉층)로 보내면 됩니다.

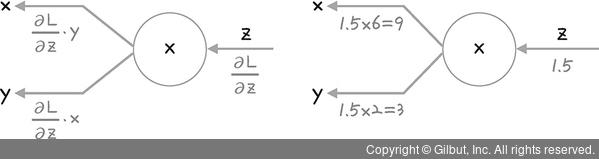
그림 9-16 | 곱셈의 노드 역전파

덧셈과 곱셈의 역전파를 묶어서 구체적인 예로 살펴볼게요. 예를 들어 q(x) = x + y, f(x) = q(x) × z 두 개의 함수가 있고 이를 계산 그래프로 그리면 다음과 같습니다.

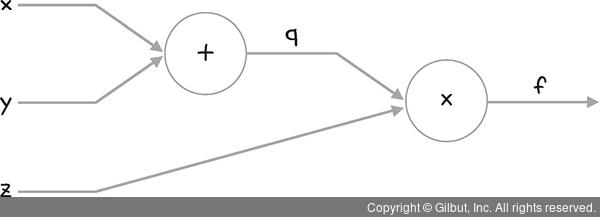
그림 9-17 | q(x) = x + y, f(x) = q(x) × z 함수의 계산 그래프 표현