1 고유 값과 고유 벡터란

고유 벡터(eigenvector)는 선형 변환을 취했을 때 방향(direction)은 변하지 않고 크기(magnitude)만 변하는 벡터를 의미합니다.

여기에서 고유 벡터의 크기가 변한다고 했는데, 얼마나 변할까요? 바로 그 변한 크기가 고유 값(eigenvalue)을 의미합니다. 고유 값이 2라면 기존 벡터 크기의 2배만큼 길어진 것이고, 고유 값이 이라면 기존 벡터 크기의 만큼 줄어든 것입니다.

이를 수학적으로 정리하면 다음과 같습니다.

정방행렬 A에 대해 A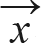 = λ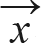 (λ는 상수)가 성립하는 0이 아닌 벡터 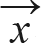가 존재할 때, λ 상수를 행렬 A의 고유 값이라고 하며, 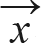를 이에 대응하는 고유 벡터라고 합니다.

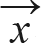A = λ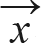 (λ는 상수)