벡터 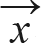 에 대해 n차 정방행렬 A를 곱하는 결과와 λ 상수를 곱하는 결과가 같습니다. 즉, 행렬 곱의 결과가 원래 벡터와 ‘방향’은 같고, ‘배율’만 λ 상수만큼 비례해서 변했다는 것을 의미합니다.
에 대해 n차 정방행렬 A를 곱하는 결과와 λ 상수를 곱하는 결과가 같습니다. 즉, 행렬 곱의 결과가 원래 벡터와 ‘방향’은 같고, ‘배율’만 λ 상수만큼 비례해서 변했다는 것을 의미합니다.
고유 값을 구하는 과정을 살펴봅시다. 고유 값을 구하는 공식은 다음과 같습니다.

이때 값이 변하지 않고 행렬이 그대로 나오게 하고자 단위행렬(I)을 곱합니다. 따라서 λ를 단위행렬과 곱합니다.
앞의 2차 정방행렬 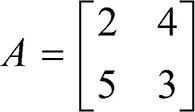 을 이용하여 고유 값을 구해 봅시다.
을 이용하여 고유 값을 구해 봅시다.
2차 정방행렬  에 대해 A
에 대해 A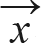 는
는  고, 이것을 풀어 보면 다음과 같습니다.
고, 이것을 풀어 보면 다음과 같습니다.


