이때 x₁이 1일 때 x₂는 -1이 되므로 고유 벡터는 다음과 같습니다.

∴ 고유 벡터는 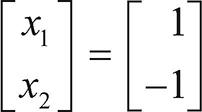입니다.

따라서 2차 정방행렬 A에 대한 특성방정식을 이용하여 고유 값 λ는 {7, -2}이며, 고유 벡터는 각각 [4 5]와 [1 -1]입니다.

파이썬에서는 다음과 같이 고유 벡터와 고유 값을 구할 수 있습니다.

In [61]:

# NumPy 라이브러리를 호출합니다
import numpy as np

# 2차원 행렬 A
# np.linalg.eig(a)는 고유 값과 고유 벡터 도출을 위한 함수입니다
a = np.array([[5, -1], [-2, 1]])
w, v = np.linalg.eig(a)

# 고유 값 구하기
print(w)
print(v)

[5.44948974 0.55051026]   --- 고유 값에 대한 결괏값

[[ 0.91209559 0.21927526] --- 고유 벡터에 대한 결괏값

 [-0.40997761 0.97566304]]

참고로 고유 벡터의 수학적 계산과 파이썬의 고유 벡터 결과가 다른 이유는 고유 벡터를 표시할 때는 보통 길이가 1인 단위 벡터가 되도록 정규화(normalization)하기 때문입니다.