2 고유 공간

고유 공간은 특정 고유 값에 대응되는 무수히 많은 고유 벡터가 이루는 공간입니다.

고유 공간은 다음 성질이 있습니다.

◼︎ ‘고유 값 λ에 대응하는 모든 고유 벡터’에 ‘영 벡터’를 첨가하여 구성된 집합입니다.

◼︎ 각각의 고유 값 λ에 대응하는 행렬 A의 고유 공간이 있습니다.

예제로 고유 공간을 확인해 볼게요.

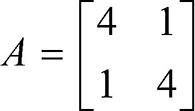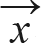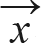일 때, A = λ를 적용하면 와 같은 수식이 성립합니다. 이때 x₁과 x₂에 다음과 같이 값을 대입하면 표 12-1과 같은 결과가 나옵니다.

표 12-1 | x₁과 x₂에 값을 대입한 결과