따라서 C₂ = 0이 성립하며, 이를 선형방정식에 대입하면 C₁ = 0입니다.

즉, C₁ = C₂ = 0으로 두 벡터는 선형 독립입니다.

또 다른 예시로, R³의 세 벡터가 선형 독립임을 확인해 봅시다.

세 벡터가 각각 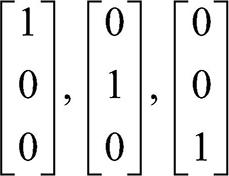일 때, 임의의 상수 C₁, C₂, C₃을 곱한 후 더해 봅시다.

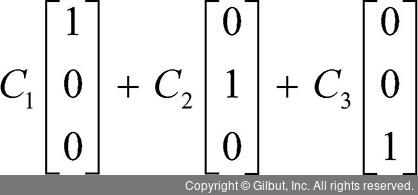
선형 독립의 정의에 따라 C₁a₁, + C₂a₂, + C₃a₃,+ …, + C_na_n = 0이 되어야 하므로 곱셈 결과는 0이 됩니다.

C₁×1 + C₂×0 + C₃×0 = 0이므로, C₁ = 0이 됩니다.

C₁×0 + C₂×1 + C₃×0 = 0이므로, C₂ = 0이 됩니다.

C₁×0 + C₂×0 + C₃×1 = 0이므로, C₃ = 0이 됩니다.

따라서 벡터 세 개는 선형 독립입니다.