그림 10-21 역시 벡터 두 개가 선형 결합을 해서 하나로 줄어듭니다. 따라서 주어진 벡터는 선형 종속입니다.

또 다른 예로 세 벡터 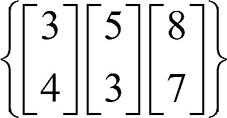이 선형 종속인지, 선형 독립인지 알아봅시다.

그림 10-22와 같이 주어진 벡터 세 개 중 두 벡터 (3, 4), (5, 3)의 합은 (8, 7)이 됩니다.

(3, 4) + (5, 3) = (8, 7)

앞서 선형 종속이 되는 필요충분조건은 S = {v₁, v₂, v₃, …, v_n}에 속하는 한 벡터가 S에 속하는 다른 벡터의 선형 결합으로 표현할 수 있어야 한다고 했습니다. 즉, 벡터 (8, 7)은 벡터 (3, 4)와 (5, 3)의 생성으로 도출 가능하기 때문에 세 벡터는 선형 종속입니다.

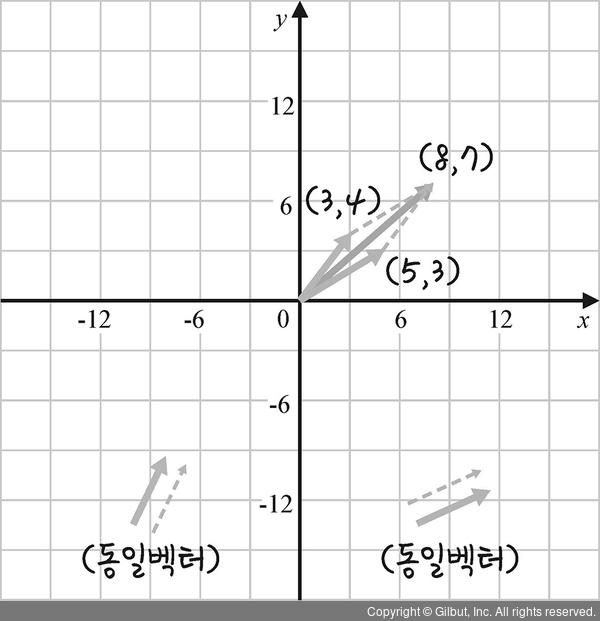
그림 10-22 | 세 벡터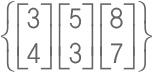

연습 문제

(1) 는 선형 독립인가요? 선형 종속인가요?

(2) 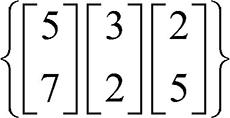는 선형 독립인가요? 선형 종속인가요?

(3) 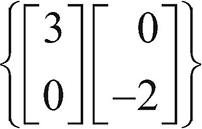는 선형 독립인가요? 선형 종속인가요?