벡터 공간의 표현

2차원(성분이 x, y로 두 개) 벡터 공간은 다음과 같이 표현합니다.

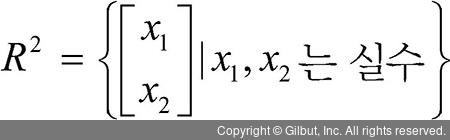
2차원 벡터 공간은 직관적으로 평면에 대한 표현으로 이해하면 쉽습니다. 성분이 세 개인 벡터 공간은 다음과 같이 표현합니다.

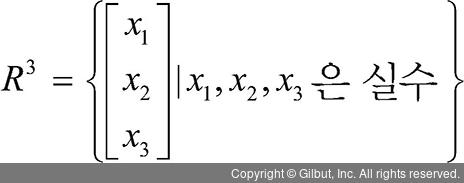
3차원 벡터 공간은 우리가 사는 공간으로 이해하면 됩니다. R³의 벡터 x = (x₁, x₂, x₃), y = (y₁, y₂, y₃)과 스칼라 k ∈ R에 대해 두 벡터의 합 x + y와 k에 의한 x의 스칼라 곱 k × x를 정리하면 다음 수식이 성립합니다.

(1) x + y = (x₁ + y₁, x₂ + y₂, x₃ + y₃)

(2) k × x = (kx₁, kx₂, kx₃)

즉, 앞의 두 연산과 함께 R³은 이 연산에 관한 실수 집합 R 위의 벡터 공간을 이룹니다.