하지만 그림 10-27에서 초록색 벡터 (-2, 2)에 0을 곱했을 때, 그 결과가 직선 t상에 존재하는지 생각하면 이해하기 쉽습니다. 혹은 회색 벡터 (2, 5)에 주황색 벡터 (-3, 1)을 더했을 때 그 결과가 직선 t상에 존재하는지 생각하면 됩니다. 두 가지 경우 모두 t 직선을 벗어난 결과를 얻습니다. 따라서 앞의 직선은 R²의 부분 공간이 아닙니다.

(2) 벡터 가 벡터 공간 v에 포함되어 있다면, 에 임의의 스칼라를 곱한 값 또한 v에 포함되어야 합니다. 즉, 다음 수식을 만족해야 합니다.

∈ v고, c가 스칼라이면 c ∈ v입니다.

이때 ‘스칼라 곱셈에 대해 닫혀 있다’고 표현하기도 합니다.

다음 좌표로 (2)를 만족하는지 확인해 보겠습니다.

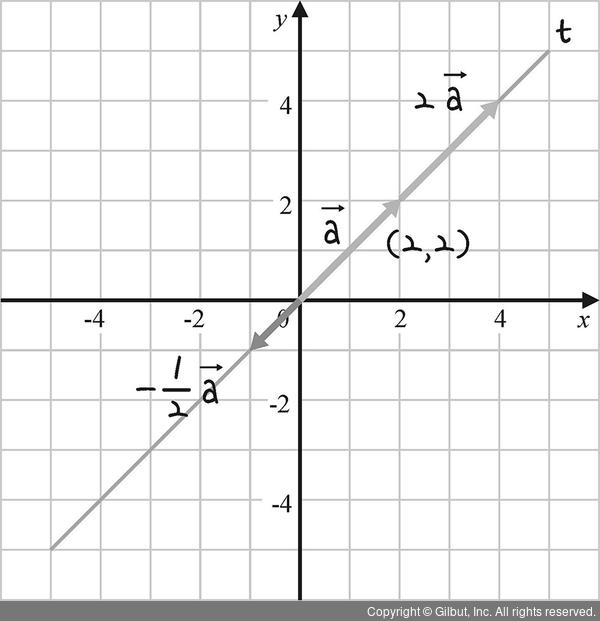
그림 10-28 | 곱셈에 닫혀 있는지 유무에 대한 좌표