스칼라 곱은 R2의 부분 공간일까요? 우선 원점인 영 벡터를 지나야 하는 (1)의 조건은 만족합니다. 벡터 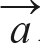 (2, 2)에 임의의 실수를 곱한 결과 역시 그림 10-28의 직선 t를 벗어나지 않기 때문에 R2의 부분 공간이라고 할 수 있습니다.
(2, 2)에 임의의 실수를 곱한 결과 역시 그림 10-28의 직선 t를 벗어나지 않기 때문에 R2의 부분 공간이라고 할 수 있습니다.
벡터 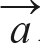 = (2, 2)라고 가정했을 때, 벡터
= (2, 2)라고 가정했을 때, 벡터 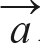 에 임의의 실수 2를 곱한 결과가 (4, 4)가 되기 때문에 직선 t를 벗어나지 않습니다. 또 벡터
에 임의의 실수 2를 곱한 결과가 (4, 4)가 되기 때문에 직선 t를 벗어나지 않습니다. 또 벡터 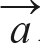 에 임의의 실수 -
에 임의의 실수 - 을 곱한 결과가 (-1, -1)이 되기 때문에 이 역시 직선 t를 벗어나지 않습니다. 따라서 ‘스칼라(임의의 실수) 곱셈’ 결과는 벡터 공간 R2의 부분 공간이 됩니다.
을 곱한 결과가 (-1, -1)이 되기 때문에 이 역시 직선 t를 벗어나지 않습니다. 따라서 ‘스칼라(임의의 실수) 곱셈’ 결과는 벡터 공간 R2의 부분 공간이 됩니다.
(3) 벡터  와
와 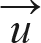 가 v에 포함되어 있다면,
가 v에 포함되어 있다면,  +
+ 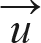 도 v에 포함되어야 합니다.
도 v에 포함되어야 합니다.
 ∈ v이고,
∈ v이고, 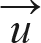 ∈ v이면
∈ v이면  +
+  ∈ v입니다.
∈ v입니다.
또 ‘덧셈에 대해 닫혀 있다’고 표현하기도 합니다.
다음 좌표로 (3)을 만족하는지 확인해 보겠습니다. 벡터 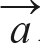 = (-5, 6)과 벡터
= (-5, 6)과 벡터 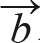 = (-10, 2)가 있을 때,
= (-10, 2)가 있을 때, 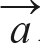 +
+ 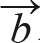 결과가 R2의 부분 공간임을 확인하면 됩니다. 그림 10-29의 주황색 벡터 실선과 점선은 크기와 방향이 같으므로 같은 벡터입니다. 동일한 이유로 초록색 벡터 실선과 점선도 같은 벡터입니다.
결과가 R2의 부분 공간임을 확인하면 됩니다. 그림 10-29의 주황색 벡터 실선과 점선은 크기와 방향이 같으므로 같은 벡터입니다. 동일한 이유로 초록색 벡터 실선과 점선도 같은 벡터입니다.
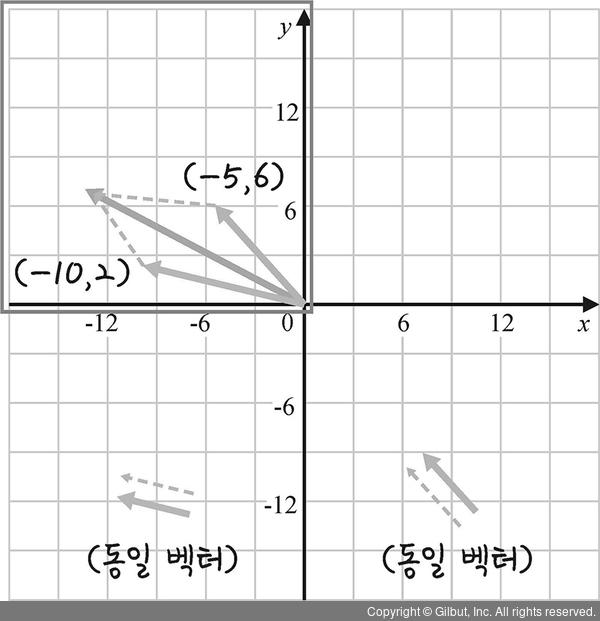
그림 10-29 | 덧셈 증명