주어진 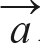, 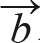는 그림 10-29에서 2사분면의 파란색 테두리를 벗어나지 않습니다. 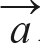+ 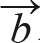결과인 (-15, 8) 역시 그림 10-29에서 2사분면의 파란색 테두리를 벗어나지 않습니다. 따라서 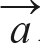, 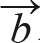는 덧셈에 대해 닫혀 있으므로 벡터 공간 R²의 부분 공간이 됩니다.

앞의 부분 공간 조건 중 (3)은 덧셈만 언급하고 있습니다. 아직 벡터 연산은 배우지 않았지만, 벡터 연산은 ‘덧셈, 뺄셈, 곱셈(내적, 외적)’으로 나눕니다. 이 세 가지 연산 중 덧셈 결과만 부분 공간의 형성 조건을 언급하고 있습니다.

그렇다면 뺄셈과 곱셈은 왜 부분 공간이 될 수 없을까요?