곱셈의 부분 공간

벡터 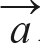= (-5, 6)과 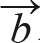= (-10, 2)가 있을 때, 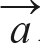· 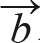결과가 왜 R²의 부분 공간이 될 수 없는지 확인해 봅시다.

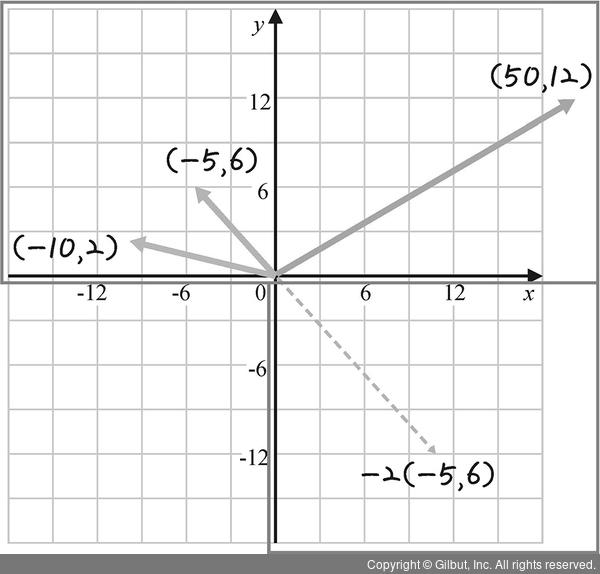
그림 10-31 | 곱셈 증명

주어진 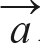, 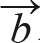는 그림 10-31에서 2사분면의 파란색 테두리를 벗어나지 않습니다. 하지만 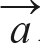· 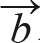결과인 (50, 12)는 1사분면으로 확장되었습니다. 또 벡터 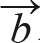에 임의의 실수 -2를 곱했을 때 4사분면으로 확장되었습니다. 따라서 두 벡터의 곱셈에서는 닫혀 있지 않으므로 벡터 공간 R²의 부분 공간이 아닙니다.