(2) 결합 법칙: (A + B) + C = A + (B + C)

예시

= (12, 17), = (2, -5), 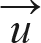= (4, -3)일 때,

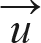( + ) + = ((12, 17) + (2, -5)) + (4, -3) = (18, 9)

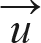+ ( + ) = (12, 17) + ((2, -5) + (4, -3)) = (18, 9)

따라서 (A + B) + C = A + (B + C) 법칙이 성립함을 확인할 수 있습니다.

(3) 벡터 덧셈의 항등원이 존재: A + 0 = A

(4) 벡터 덧셈의 역원이 존재: A + (-A) = 0

NOTE

역원

연산 결과로 항등원을 만드는 원소를 역원(inverse element)이라고 하며, 다음과 같이 표기합니다.

 

S^-1

 

그림 10-36과 같이 a + (-a) = 0에서 덧셈의 역원은 부호가 반대인 수(반수)입니다. 참고로 곱셈의 역원은 부호가 반대인 수(역수)입니다.

예를 들어 a의 역원은 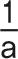이 되므로 a + 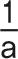= 1이 됩니다

(이때 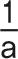= a^-1으로 이해하면 됩니다).

 

그림 10-36 | 덧셈에 대한 역원