벡터의 내적

벡터의 내적은 벡터 공간에서 정의된 이중 선형함수의 일종으로 inner product 또는 dot product라고 합니다.

벡터의 내적을 구하는 방법은 두 가지입니다. 첫 번째 방법은 좌표 값의 각 성분을 곱해서 더하는 것입니다. 두 벡터 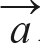= (a₁, a₂, a₃, …, a_n), 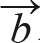= (b₁, b₂, b₃, …, b_n)의 내적은 수식 10.10처럼 정의합니다.

수식 10.10

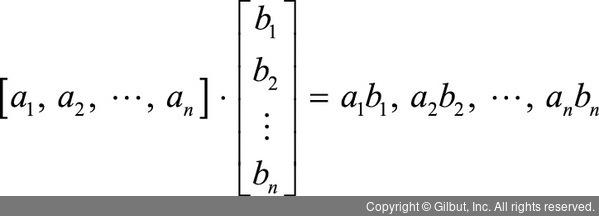= 스칼라

수식 10.10에 구체적인 숫자를 대입해 보겠습니다. 두 벡터 (6, 6)과 (12, 0)이 있을 때 벡터의 내적은 다음과 같이 구할 수 있습니다.

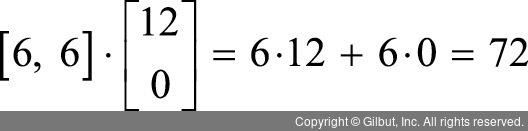
파이썬에서는 벡터의 내적을 다음과 같이 구현합니다.

In [31]:

# NumPy 라이브러리를 이용한 벡터의 합
import numpy as np

# [6, 6] 리스트를 NumPy의 배열 객체로 변화한 후 u 변수에 저장합니다
# [12, 0] 리스트를 NumPy의 배열 객체로 변화한 후 v 변수에 저장합니다
u = np.array([6, 6])
v = np.array([12, 0])

# numpy.dot()으로 벡터의 내적을 구한 후 uv 변수에 저장합니다
uv = np.dot(u, v)
print(uv)

72