벡터 A, B가 이루는 각이 θ일 때, 한 벡터(A)를 다른 벡터(B)로 정사영시켜서(|A|cosθ) 곱합니다(단 두 벡터의 방향이 같아야 합니다). 즉, A와 B의 내적 ·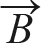는 다음과 같습니다.

·

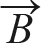
= B의 크기 × D의 크기

= |B|×|A|cosθ

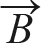= ||||cosθ

이때 두 벡터가 이루는 각이 90도라면 직선과 평면이 평행하기 때문에 내적 값은 0입니다.

벡터 내적의 조건은 다음과 같습니다.

◼︎ 벡터 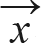와 의 차원(길이)이 같아야 합니다.

즉, 앞 벡터의 열 개수와 뒤 벡터의 행 개수가 일치해야 합니다.

◼︎ 앞의 벡터가 행 벡터고 뒤의 벡터가 열 벡터이어야 합니다.

◼︎ 두 벡터 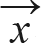와 의 내적 결과는 숫자 하나(스칼라(scalar))입니다.

즉, 다음과 같은 수식이어야 벡터의 내적이 가능합니다.

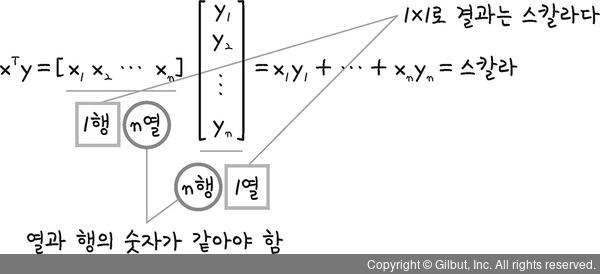
그림 10-41 | 벡터 내적의 조건