벡터의 외적

벡터의 외적은 3차원 공간에 있는 벡터 간 연산 중 하나입니다. 벡터 간 연산의 결과이기 때문에 벡터곱(vector product)이라고 합니다. 이때 두 3차원 벡터의 외적 결과가 3차원인 경우를 벡터곱(cross product)이라고 하며, 외적 결과가 행렬인 경우를 외적(outer product)이라고 합니다. 내적과 마찬가지로 벡터곱과 외적은 모두 동일한 의미로 사용합니다.

벡터의 외적은 내적과 달리 연산 결과가 벡터이기 때문에 다음과 같이 방향과 크기를 동시에 갖습니다.

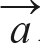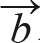◼︎ 방향: 두 벡터 와 에 동시에 수직

◼︎ 크기: 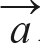와 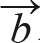크기를 변으로 하는 평행사변형의 넓이

따라서 벡터의 외적은 수식 10.11과 같은 공식이 성립합니다.

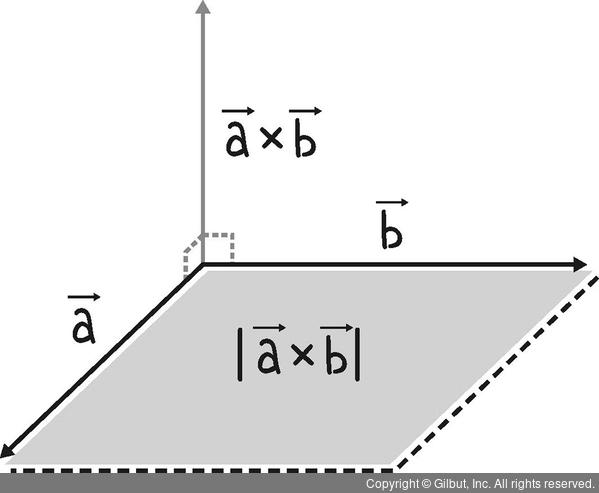
그림 10-42 | 벡터의 외적