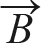Out [41]:
[-2, 4, -2]
In [42]:
# NumPy를 이용한 벡터 외적 계산 import numpy as np print(np.cross(a,b)) # cross() 함수를 이용한 결과
Out [42]:
[-2 4 -2]
지금까지 내적과 외적을 배웠는데, 표 10-9에서 이 둘의 차이를 다시 확인하고 넘어가세요.
|
구분 |
내적 |
외적 |
|
명칭 |
inner product, dot product, Scalar product |
outer product, cross product, Vector product |
|
표기 |
|
|
|
공식 |
|
|
|
대상 벡터 |
|
|
|
계산 결과 |
스칼라 |
벡터 |
|
최대, 최소 |
두 벡터가 평행일 때 최대, 수직일 때 최소 |
두 벡터가 수직일 때 최대, 평행일 때 최소 |
|
활용 |
벡터의 길이, 벡터 간 각도 |
삼각형, 평행사변형 넓이 계산 |
표 10-9 | 벡터의 내적과 외적
연습 문제
다음 문제에서 벡터의 외적을 계산하세요.
(1) 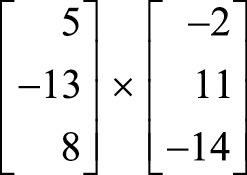
(2) 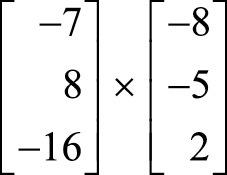
 ·
·