벡터 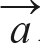는 x축, 벡터 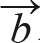는 y축에 있습니다. 두 벡터가 이루는 각도는 직각이며, 두 벡터를 더했을 때 수식 10.13처럼 피타고라스 정리에 따라 직각삼각형이 됩니다.

수식 10.13

||a||² + ||b||² = ||a + b||²

2차원 벡터의 직교는 그림 10-46과 같이 좌표 평면에서 쉽게 확인할 수 있으나 n차원에서 두 벡터가 직교인지는 내적으로 확인할 수 있습니다.

수식 10.14

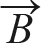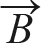· = ||||cosθ

내적을 다시 정리하면 다음과 같습니다.

수식 10.14에서 두 벡터 사이의 각도에 대한 코사인 때문에 두 벡터가 직교할 경우 그 결괏값이 0이 나오는 것입니다(∵ cosine 90° = 0). 따라서 다음과 같이 두 벡터가 직교일 경우 두 벡터의 내적은 0이 됩니다.

그림 10-46에서 벡터와 삼각형을 수식으로 표현하면 다음과 같습니다.

수식 10.15

||x||² + ||y||² = ||x + y||²