이때 벡터 x와 y의 크기를 제곱한 값은 벡터 x + y(삼각형의 대각선)의 크기를 제곱한 값과 같습니다.

예를 들어 두 벡터 x와 y를 사용하여 내적을 구해 봅시다.

일 때, ||x||² + ||y||² = ||x + y||²을 적용하면 다음과 같습니다.

수식 10.16

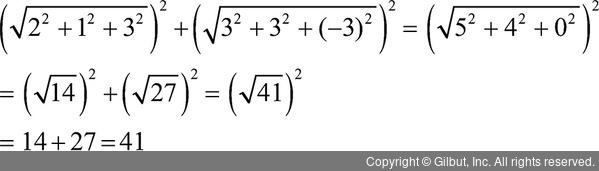
이때 직각삼각형에서 직교하는 벡터 사이에서만 앞의 식이 성립함을 알아 두세요. 앞의 풀이는 일반적인 방법이며, 선형대수적인 방법으로 표현하면 다음과 같습니다.

수식 10.17

||x||² + ||y||² = ||x + y||²

↓

x^Tx + y^Ty = (x + y)^T(x + y)

수식 10.17에 구체적인 숫자를 대입해서 이해해 보겠습니다.

일 때, x^Tx + y^Ty = (x + y)^T(x + y)를 적용하면 다음과 같습니다.

수식 10.18

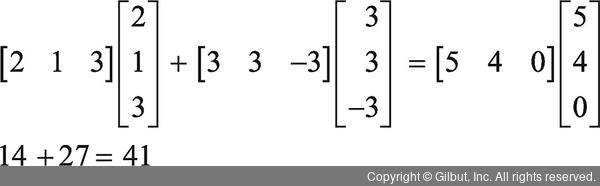
즉, 수식 10.16과 수식 10.18의 결과가 같다는 것을 알 수 있습니다. 이것으로 우리가 알고 있던 피타고라스 정리인 수식 10.15와 벡터 방식으로 표현한 수식 10.17이 같음을 확인할 수 있습니다.