행렬 A는 열을 세 개 가졌고, 각 열은 원소 세 개로 이루어져 있는 3차원 공간 R³의 부분 공간입니다. A의 열을 선형 결합 형태로 표현하기 위해 A의 열 부분 공간을 상세히 살펴봅시다.

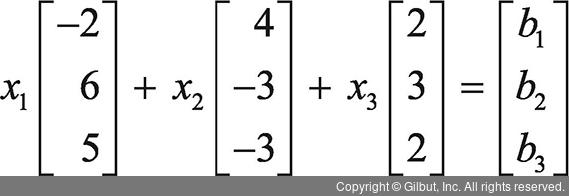
수식 10.20의 A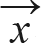 = b는 방정식 세 개와 미지수 세 개를 갖습니다. 미지수 세 개는 x = [x₁, x₂, x₃]을 의미합니다. 벡터 b가 어떤 값을 가져야 해를 구할 수 있을까요? 쉽게 생각할 수 있는 답은 b 벡터가 모두 0인 경우입니다. 즉, b = [0 0 0]일 때입니다.

또 다른 경우는 b = [-2 6 5]일 때 x = [1 0 0]이 되며, 이때 b는 A의 첫 번째 열과 같습니다. 같은 방법으로 x = [0 1 0]과 x = [0 0 1]이 되는 경우도 가능합니다. 따라서 그림 10-55와 같이 정리할 수 있습니다.

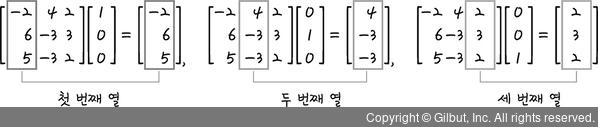
그림 10-55 | A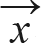 = b에 대한 해