3 행렬의 영 공간

행렬의 영 공간(null space)은 행렬 A와 벡터 x를 곱했을 때 그 결과가 0이 되는 모든 열 벡터 x의 집합을 의미합니다. 즉, 선형방정식 A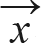 = 0의 해(solution)들이 이루는 공간을 의미합니다. 예를 들어 다음과 같이 행렬 A 곱하기 벡터 x가 0이 되는 모든 열 벡터 x의 집합을 영 공간이라고 합니다.

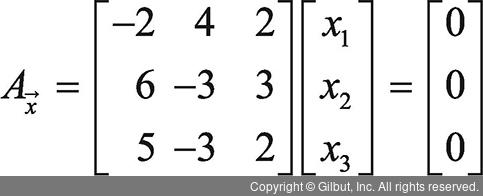
이때 생각해 볼 수 있는 x 값은 영 벡터, 즉 x = [0 0 0]입니다. 또 다른 영 공간의 조건을 생각해 볼까요? 행렬 A의 첫 번째 열(col1)과 두 번째 열(col2)을 더하고, 세 번째 열(col3)에 -1을 곱하면 그 결과는 영 벡터가 됩니다. 즉, x = [1 1 -1]입니다. 또 다른 해는 x = [1 1 -1]에 c 상수를 곱하는 것입니다.

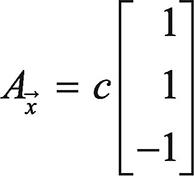
이것으로 영 공간은 3차원 공간 R³의 부분 공간이라는 것을 확인할 수 있습니다. 참고로 3차원 공간에서 영 공간은 직선으로 표현합니다.