그렇다면 치역은 어떨까요? 구체적인 사례로 치역을 확인해 보겠습니다. 예를 들어 F: (3, 2) → (5, -1, 6)은 다음과 같이 표현할 수 있습니다.

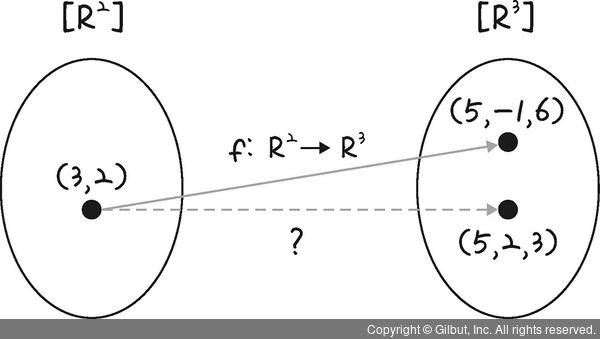
그림 11-3 | F: (3, 2) → (5, -1, 6)

집합 R³에서 (5, 2, 3)은 치역이 될 수 있을까요? 결론부터 말하면, (5, -1, 6)만 치역이 가능합니다. 치역은 X 값에 대응되는 Y 값 중에서 X와 연결된 값들이라고 정의했습니다. 그림 11-3의 함수 f(x₁, x₂) = (x₁ + x₂, x₂ - x₁, 2x₁)에 대해 Y 값의 결과는 다음과 같습니다.

f(x₁, x₂) = (x₁ + x₂, x₂ - x₁, 2x₁) → f(3, 2) = (3 + 2, 2 - 3, 2 × 3) = (5, -1, 6)

따라서 Y 값 (5, -1, 6)에 대해서는 치역이 가능합니다. (5, 2, 3)이 치역이 될 수 없는 이유는 함수 f(x₁, x₂) = (x₁ + x₂, x₂ - x₁, 2x₁)의 결과로 (5, 2, 3)이 나올 수 없기 때문입니다. 즉, (5, 2, 3)은 공역은 될 수 있으나 치역은 될 수 없습니다.

연습 문제

F: A → B에서 x → x²일 때 정의역, 공역, 치역, 2의 상, 1의 원상, 9의 원상을 구하세요.