행렬 A에 임의의 행렬 B를 곱하는 AB는 벡터 B를 3차원에서 2차원으로 변환시키는 것을 의미합니다. 즉, 선형 변환은 3차원에서 2차원으로 변환처럼 한 벡터 공간에서 다른 벡터 공간으로 이동하는 규칙 정도로 이해합니다.

선형 변환도 일종의 함수이기 때문에 선형 변환 역시 합성 개념으로 이해할 수 있습니다. 다음과 같은 선형 변환을 가정해 볼게요(T₁의 공역은 T₂의 정의역과 같습니다).

T₁: Rⁿ → R^k, T₂: R^k → R^m

여기에서 Rⁿ상의 벡터 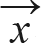에 대해 T₁(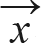)를 계산하고, 그 후 R^k상의 벡터 T₁(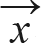)를 가지고 R^m상의 최종적인 벡터 T₂(T₁(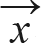))를 계산해 봅시다. 즉, 다음과 같은 선형 변환의 합성이 가능합니다.

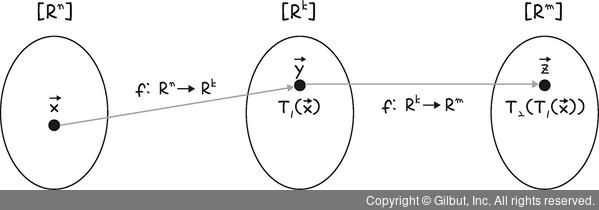
그림 11-7 | 선형 변환의 합성

계산 과정은 Rⁿ상의 벡터 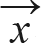에 T₁을 적용한 후, T₂를 적용하는 과정으로 결국 전체 과정은 Rⁿ → R^m인 변환으로 볼 수 있습니다. 이러한 Rⁿ → R^m으로 변환을 T₂와 T₁의 합성이라고 하며, 다음과 같이 표기합니다(T₂ 서클(circle) T₁이라고 읽습니다).

T₂ ◦ T₁