함수 f: X → Y가 일대일 대응일 때, Y의 임의의 원소 y에 대해 y = f(x)인 X의 원소 x는 하나만 있습니다. 이때 y에 대해 x를 대응시키면 Y를 정의역, X를 공역으로 하는 새로운 함수를 만들 수 있는데, 이를 f의 역함수라고 하며 다음과 같이 표현합니다.

f^-1: Y → X

따라서 다음 공식이 성립합니다.

y = f(x) ⇔ x = g(y) ⇔ x = f^-1(y)

다음은 역함수의 추가적인 성질입니다.

[역함수의 성질]

(1) (f^-1)^-1 = f

(2)

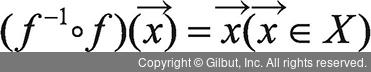
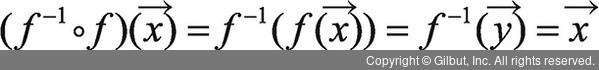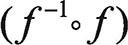에서 는 X에서의 항등함수를 의미합니다.

(3)

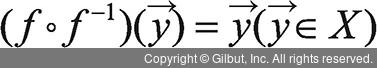
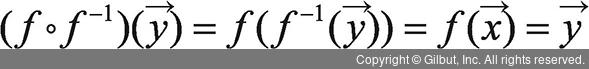에서 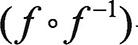은 Y에서의 항등함수를 의미합니다.

정의역 X와 공역 Y가 실수 전체의 집합일 때 (2), (3)을 구분하는 것은 의미가 없습니다. 따라서 f ◦ f^-1 = f^-1 ◦ f = I가 됩니다(I는 항등함수의 표현입니다).

참고로 모든 함수가 역함수를 갖는 것은 아닙니다. 앞의 성질을 만족할 때 역함수를 가지며, 이때 함수를 가역함수라고 합니다.