일대일 함수와 일대일 대응

• 일대일 함수: 집합 X의 임의의 원소 x₁, x₂에 대해 x₁ ≠ x₂일 때 f(x₁) ≠ f(x₂)인 함수

• 일대일 대응: 일대일 함수 + (공역 = 치역)

이제 일대일 함수와 일대일 대응을 한번 구분해 볼까요? 집합 X의 원소 x₁에 대해 f(x₁) ∈ Y이면 함수입니다. 이때 x₁ ≠ x₂일 때 f(x₁) ≠ f(x₂)이면 일대일 함수고, 공역 = 치역이면 일대일 대응입니다.

그림 11-13은 집합 X의 원소 다섯 개에 Y의 원소 두 개가 대응하므로 함수입니다(f(1) = f(2)이므로 그냥 함수가 됩니다).

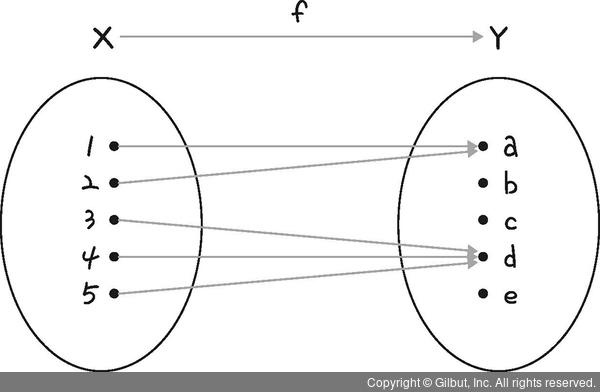
그림 11-13 | f 함수

그림 11-14는 집합 X의 원소에 대응하는 집합 Y의 원소가 다 다릅니다. 그런데 공역은 {a, b, c, d, e}고 치역은 {a, b, c, d}로 공역 ≠ 치역이므로 일대일 함수입니다.

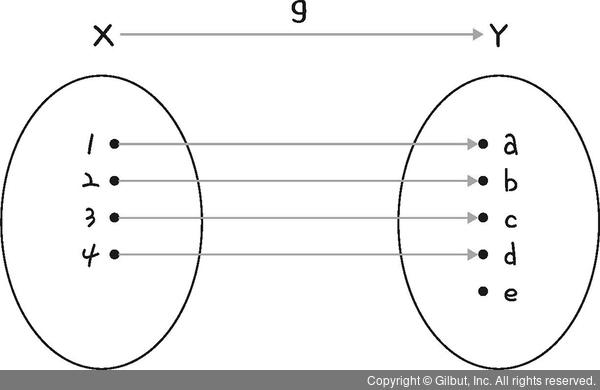
그림 11-14 | g 함수