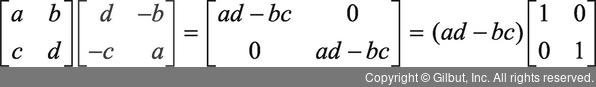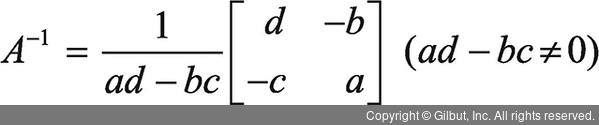참고로 숫자에서는 a^-1 = 이 성립하지만, 행렬에서는 A^-1 = 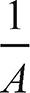이 성립하지 않습니다. 또 일반적으로 행렬의 곱셈에 대한 성질에서는 AB ≠ BA이지만, 행렬과 그 역행렬에서는 AA^-1 = A^-1A가 성립합니다(동일하게 단위행렬을 도출하므로 AA^-1 = A^-1A가 성립합니다).

행렬 A가 2 × 3이고, A^-1이 3 × 2라면 AA^-1 = E가 되는데, 이때 E는 2차 정사각행렬이 됩니다.

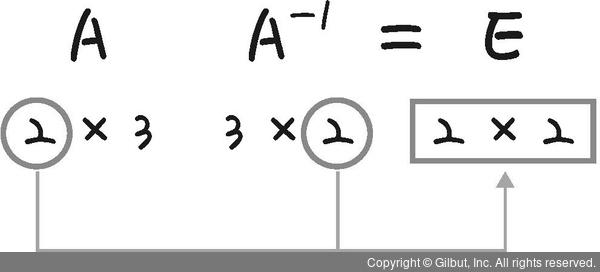
그림 11-25 | 역행렬

반대로 A^-1A = E에서 E는 3차원 정사각행렬이 됩니다. AA^-1과 A^-1A 모두 단위행렬 E를 갖지만 서로 다른 행렬입니다. 따라서 곱셈 결과가 똑같은 n차 단위행렬이 되려면 A와 A^-1도 n차 정사각행렬이어야 합니다.

역행렬 공식

역행렬 공식은 다음과 같습니다.