수식이 어렵게 보일 수 있기 때문에 예시로 알아봅시다. 다음과 같이 행렬 A가 있다고 할게요.

일 때, det A는 다음과 같이 계산할 수 있습니다.

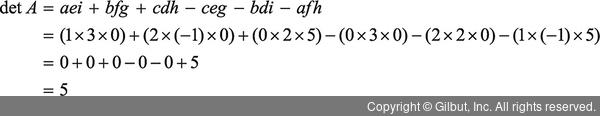
전치행렬과 행렬식을 이용하면 다음과 같은 전치행렬 성질을 도출할 수 있습니다.

det(A^T) = det(A)

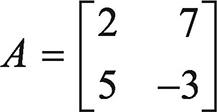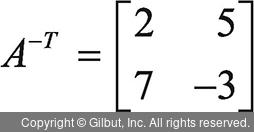예를 들어 행렬 이고, 이면,

det(A) = ad - bc = -6 - 35 = -41, det(A^T) = ad - bc = -6 - 35 = -41입니다.

따라서 det(A) = det(A^T)이 성립합니다.

행렬식은 정사각행렬이 나타내는 선형 변환이 부피를 확대시키는 정도를 표현할 때 주로 사용합니다.

연습 문제

의 det A를 구하세요.