2 수열의 극한과 발산

수열의 극한

수열의 극한과 발산은 ‘둘째마당 미분’에서 학습했던 함수의 극한과 발산 개념이 동일합니다. 발산이란 어떤 수에 한없이 가까워지는 것이기 때문에 수열의 극한 역시 어떤 수에 한없이 가까워지는 값입니다. a_n에서 n이 커짐에 따라 고정된 값 a에 가까워진다면 a_n이 a로 수렴한다고 하며, a를 a_n의 극한이라고 합니다. 수열의 극한은 다음과 같이 표현합니다.

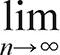a_n = a 또는 n → ∞일 때, a_n → a

예를 들어 다음과 같은 수열 {a_n}과 {b_n}이 있다고 가정합니다.

이때 n이 커짐에 따라 일반항 a_n과 b_n 값의 변화는 그림 13-4와 같습니다.

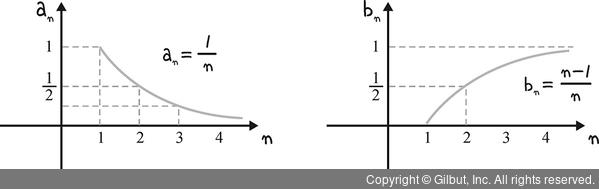
그림 13-4 | 수열의 수렴