일반적으로 수열 {an}에서 n 값이 한없이 커질 때, 일반항 an 값이 양수이면서 그 값이 한없이 커지면 수열 {an}은 양의 무한대로 발산한다고 하며 다음과 같이 나타냅니다.
n → ∞일 때, an → ∞ 또는 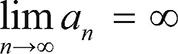
또 수열 {bn}에서 n 값이 한없이 커질 때, 일반항 bn 값이 음수이면서 그 절댓값이 한없이 커지면 수열 {bn}은 음의 무한대로 발산한다고 하며 다음과 같이 나타냅니다.
n → ∞일 때, bn → -∞ 또는 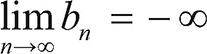
예를 들어 수열 {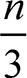 }은 양의 무한대로 발산하므로 다음과 같이 표현할 수 있습니다.
}은 양의 무한대로 발산하므로 다음과 같이 표현할 수 있습니다.
n → ∞일 때, 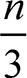 → ∞ 또는
→ ∞ 또는 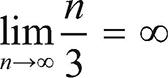
또 수열 {-n2}은 음의 무한대로 발산하므로 다음과 같이 표현합니다.
n → ∞일 때, -n2 → -∞ 또는 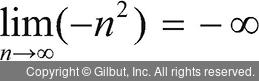
수열의 수렴과 발산을 정리하면 다음과 같습니다.
(1) 수렴: 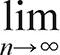 an = a (단 a는 실수)
an = a (단 a는 실수)
(2) 발산
◼︎ 양의 무한대로 발산: 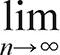 an = ∞
an = ∞
◼︎ 음의 무한대로 발산: 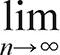 an = -∞
an = -∞
◼︎ 진동