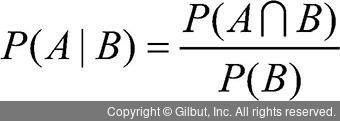베이지안 확률

두 확률변수의 사전 확률과 사후 확률 간 관계를 나타내는 정리로 사전 확률 P(A)와 우도 확률 P(B|A)를 안다면 사후 확률 P(A|B)를 알 수 있습니다. 즉, 베이지안 확률은 다음과 같이 조건부 확률로 나타내며, 정보를 업데이트하면서 사후 확률 P(A|B)를 구하는 것입니다.

그림 14-5 | 베이지안 확률

◼︎ P(A), 사전 확률(prior probability): 결과가 나타나기 전에 결정된 원인(A)의 확률

◼︎ P(B|A), 우도 확률(likelihood probability): 원인(A)이 발생했다는 가정하에 결과(B)가 발생할 확률

◼︎ P(A|B), 사후 확률(posterior probability): 결과(B)가 발생했다는 가정하에 원인(A)이 발생했을 확률

◼︎ P(B), 주변 우도(marginal probability): 사건(B)의 발현 확률

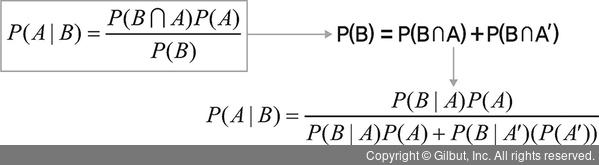
베이지안 확률을 위한 계산식 P(B)는 다음과 같이 A 및 A 여집합과 P(B) 사이의 교집합으로 구할 수 있습니다.