그렇다면 왜 확률변수와 확률함수는 통계에서 필요할까요? 확률함수는 확률변수가 일어날 확률을 나타내는 함수이므로 특정 확률변수의 확률함수를 알고 있다면 특정 사건이 일어날 확률을 예측할 수 있습니다.
파이썬의 SciPy 라이브러리에서 제공하는 stats 서브패키지는 확률분포를 분석할 수 있는 다양한 기능을 제공합니다.
In [9]:
# stats 서브패키지를 호출합니다 # 한글 깨짐을 방지하는 코드 import matplotlib as mpl import matplotlib.pylab as plt from matplotlib import font_manager font_fname = 'C:/Windows/Fonts/malgun.ttf' font_family = font_manager.FontProperties(fname=font_fname).get_name() plt.rcParams["font.family"] = font_family
In [10]:
from scipy import sp import seaborn as sns import numpy as np import matplotlib as mpl import matplotlib.pylab as plt %matplotlib inline # 확률질량함수는 SciPy의 stats 서브패키지에 binom 클래스로 구현합니다 N = 10 # 전체 시도 횟수 mu = 0.6 # 베르누이 확률분포의 기댓값 rv = sp.stats.binom(N, mu) xx = np.arange(N + 1) # 그래프를 표현할 때는 matplotlib을 사용합니다 plt.bar(xx, rv.pmf(xx), align="center") # 확률질량함수 기능을 갖는 pmf를 사용합니다 plt.xlabel("표본값") plt.ylabel("$P(x)$") plt.title("확률질량함수 pmf") plt.show()
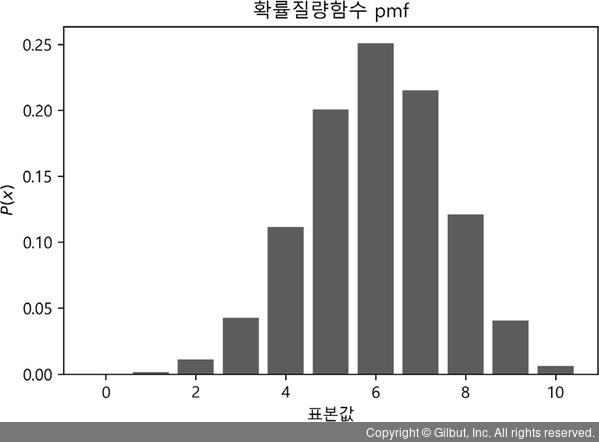
그림 15-5 | 확률밀도함수