확률밀도함수

연속확률변수는 확률변수가 취할 수 있는 값이 연속적이며 무한하기 때문에 분포를 표현하는 것이 불가능합니다. 이산형처럼 특정한 확률변수 하나에 특정한 확률 값이 대응된다면, 어떤 확률변수가 특정한 구간 안에 포함될 확률은 무한대가 되어 버립니다(확률변수가 취할 수 있는 값이 무한 개이기 때문입니다). 연속형 확률변수의 이러한 문제를 해결하려면 확률밀도함수(Probability Density Function, PDF)가 필요합니다.

확률밀도함수는 특정 구간에 속할 확률을 계산하는 함수이며, 함수가 나타내는 그래프에서 ‘특정 구간에 속한 넓이 = 특정 구간에 속할 확률’이 되는 함수입니다.

확률밀도함수의 조건은 다음과 같습니다.

(1) 모든 x 값에 대해 f(x) ≥ 0입니다. 즉, x의 모든 실수 값에 대해 확률밀도함수는 0 이상입니다.

(2) x의 모든 가능한 값의 확률은 적분 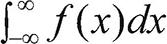로 구하며, 이 값은 항상 1입니다.

(3) 구간 (a, b)의 확률은 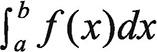입니다. 즉, 구간 (a, b)에 대한 x의 확률은 그림 15-5와 같이 해당 구간에서 확률밀도함수 f(x)로 만들어지는 면적의 크기입니다.

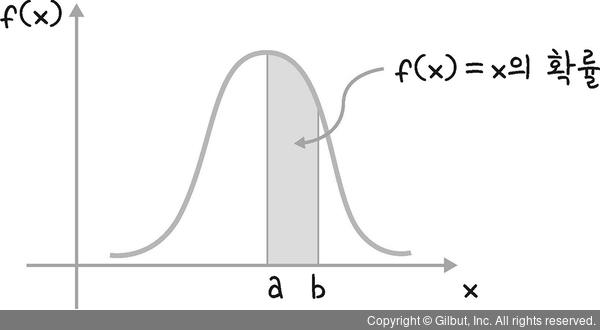
그림 15-6 | 확률분포 유형