그런데 각 집단의 평균과 표준편차가 각각 다르기 때문에 데이터를 비교하기 어렵습니다. 예를 들어 A반 수학 시험 결과는 평균이 80점이고 표준편차가 40점, B반 수학 시험 결과는 평균이 60점이고 표준편차가 12점이라고 할 때 어느 반의 수학 점수가 더 좋을까요? A와 B반의 수학 점수 데이터의 분포가 달라서 직관적으로 판단하기 어렵습니다. 따라서 모수 값(평균, 표준편차)이 다른 정규분포를 가진 집단을 서로 비교하기 위해 정규분포를 표준화해야 하는데, 이것을 표준정규분포(standard normal distribution)라고 합니다.

표준정규분포

그렇다면 어떻게 서로 다른 모양의 정규분포를 표준화할 수 있을까요? 결론부터 말하면, 정규분포의 평균을 ‘0’으로 만들고 표준편차를 ‘1’로 만들어서 표준화할 수 있습니다.

평균을 0으로 만들고 표준편차를 1로 만드는 방법은 간단합니다. 다음과 같이 수집한 개별 데이터의 확률변수 X에서 그 데이터 전체의 평균(μ)을 빼고 표준편차(σ)로 나누면 됩니다.

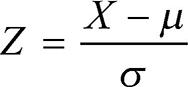
개별 데이터에서 전체 데이터의 평균만큼 뺐기 때문에 개별 데이터의 평균을 다시 구하면 0이 됩니다. 즉, 0으로 수평 이동한 것이라고 보면 됩니다. 이렇게 표준화된 개별 데이터를 표준화 점수(Z-score)라고 하며, 표준화 점수는 평균이 0이고 표준편차가 1인 정규분포의 확률변수가 됩니다.