선형함수와 비선형함수

선형회귀 모델은 ‘회귀계수(regression coefficient)를 선형 결합으로 표현할 수 있는 모델’입니다(계수들이 덧셈과 뺄셈으로만 결합되어 있는 것을 의미합니다). 즉, 독립변수가 일차식인지, 이차식인지, 로그함수인지가 중요한 것이 아니라 추정할 대상인 파라미터가 어떻게 생겼느냐의 문제입니다. 예를 들어 다음 함수는 모두 선형회귀식입니다.

• y = a₀ + a₁x₁

• y = a₀ + a₁x₁ + a₁x₂

•y = a₀ + a₁x₁ + a₂x₁³

마지막 예시는 독립변수인 x를 기준으로 생각하면 x³이기 때문에 비선형이라고 생각하기 쉽지만, 회귀 모델의 선형성은 x가 아닌 회귀계수인 a₀, a₁, a₂를 기준으로 생각해야 하기 때문에 모두 선형회귀식입니다.

그렇다면 비선형회귀 모델은 무엇일까요? 비선형 모델은 데이터를 어떻게 변형하더라도 파라미터를 선형 결합 식으로 표현할 수 없는 모델을 의미합니다.

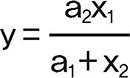
이 수식은 x, y를 아무리 변경하더라도 파라미터를 선형회귀식으로 표현할 수 없습니다.

선형회귀 모델은 파라미터 계수에 대한 해석이 단순하지만, 비선형 모델은 형태가 복잡할 경우 해석하기 어렵기 때문에 통계 모델링에서는 비선형회귀 모델을 잘 사용하지 않습니다.

마지막으로 로지스틱 회귀 모델은 무엇일까요? 로지스틱 회귀 모델의 식 자체는 비선형이지만, 로그 변환으로 계수가 선형적인 성질을 갖도록 하기 때문에 일반화된 선형 모델이라고 합니다. 특히 로지스틱 회귀 모델은 종속변수가 범주형일 때만 사용할 수 있습니다(분류하려는 범주를 성공/실패, 예/아니요, 남/여 등 두 가지 범주로 나누었을 때 적용 가능합니다).