3.2.3 주성분 분석(PCA)
▼ 표 3-13 PCA를 사용하는 이유와 적용 환경
|
왜 사용할까? |
주어진 데이터의 간소화 |
|
언제 사용하면 좋을까? |
현재 데이터의 특성(변수)이 너무 많을 경우에는 데이터를 하나의 플롯(plot)에 시각화해서 살펴보는 것이 어렵습니다. 이때 특성 p개를 두세 개 정도로 압축해서 데이터를 시각화하여 살펴보고 싶을 때 유용한 알고리즘입니다. |
변수가 많은 고차원 데이터의 경우 중요하지 않은 변수로 처리해야 할 데이터양이 많아지고 성능 또한 나빠지는 경향이 있습니다. 이러한 문제를 해결하고자 고차원 데이터를 저차원으로 축소시켜 데이터가 가진 대표 특성만 추출한다면 성능은 좋아지고 작업도 좀 더 간편해집니다. 이때 사용하는 대표적인 알고리즘이 PCA(Principal Component Analysis)입니다. 즉, PCA는 고차원 데이터를 저차원(차원 축소) 데이터로 축소시키는 알고리즘입니다.
차원 축소 방법은 다음과 같습니다.
데이터들의 분포 특성을 잘 설명하는 벡터를 두 개 선택
다음 그림에서 e1과 e2 두 벡터는 데이터 분포를 잘 설명합니다. e1의 방향과 크기, e2의 방향과 크기를 알면 데이터 분포가 어떤 형태인지 알 수 있기 때문입니다.
벡터 두 개를 위한 적정한 가중치를 찾을 때까지 학습을 진행
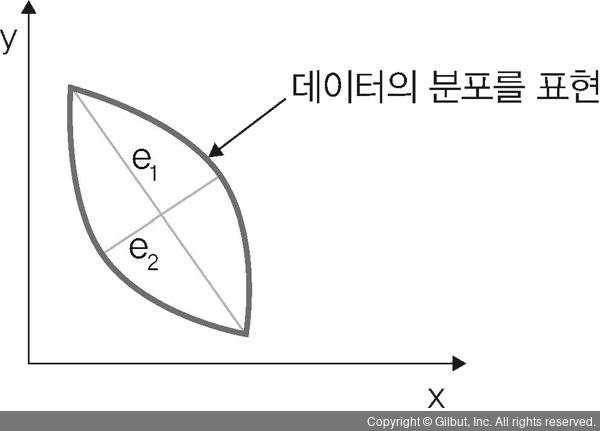
▲ 그림 3-41 2D에서 PCA 예시