즉, PCA는 데이터 하나하나에 대한 성분을 분석하는 것이 아니라, 여러 데이터가 모여 하나의 분포를 이룰 때 이 분포의 주성분¹²을 분석하는 방법입니다.

예를 들어 코드는 간단하게 다음과 같이 구현할 수 있습니다.

pca = decomposition.PCA(n_components=1)
pca_x = pca.fit_transform(x_std)

result = pd.DataFrame(pca_x, columns=['dog'])
result['y-axis'] = 0.0
result['label'] = Y

sns.lmplot('dog', 'y-axis', data=result, fit_reg=False,
           scatter_kws={"s":50}, hue='label');

밀도 기반 군집 분석과 PCA 예제를 묶어서 진행해 보겠습니다. 밀도 기반 군집 분석을 이용하여 클러스터링을 진행하겠지만, 시각화를 위해 PCA를 사용해 보겠습니다. 이번 예제의 목표는 훈련 데이터를 정확하게 클러스터링하는 것입니다.

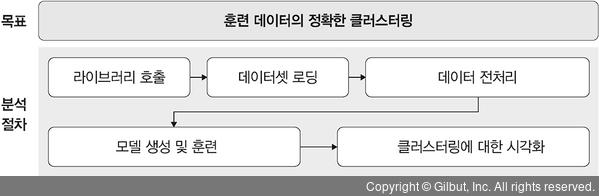
▲ 그림 3-42 밀도 기반 군집 분석과 PCA 예제