코드를 실행하면 다음 그림과 같이 적당한 K 값이 출력됩니다.

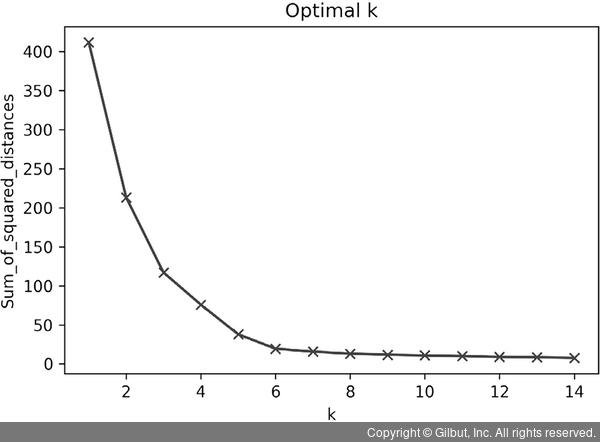
▲ 그림 3-34 K-평균 군집화 예제 실행 결과

① 거리 제곱의 합(Sum of Squared Distances, SSD)은 x, y 두 데이터의 차를 구해서 제곱한 값을 모두 더한 후 유사성을 측정하는 데 사용됩니다. 즉, 가장 가까운 클러스터 중심까지 거리를 제곱한 값의 합을 구할 때 사용하며, 다음 수식을 씁니다.

K가 증가하면 거리 제곱의 합은 0이 되는 경향이 있습니다. K를 최댓값 n(여기에서 n은 샘플 개수)으로 설정하면 각 샘플이 자체 클러스터를 형성하여 거리 제곱 합이 0과 같아지기 때문입니다.

출력 그래프는 클러스터 개수(x축)에 따른 거리 제곱의 합(y축)을 보여 줍니다. K가 6부터 0에 가까워지고 있으므로 K=5가 적정하다고 판단할 수 있습니다.