손실 함수

경사 하강법은 학습률(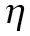, learning rate)²과 손실 함수의 순간 기울기를 이용하여 가중치를 업데이트하는 방법입니다. 즉, 미분의 기울기를 이용하여 오차를 비교하고 최소화하는 방향으로 이동시키는 방법이라고 할 수 있습니다. 이때 오차를 구하는 방법이 손실 함수입니다.

즉, 손실 함수는 학습을 통해 얻은 데이터의 추정치가 실제 데이터와 얼마나 차이가 나는지 평가하는 지표라고 할 수 있습니다. 이 값이 클수록 많이 틀렸다는 의미이고, 이 값이 ‘0’에 가까우면 완벽하게 추정할 수 있다는 의미입니다. 대표적인 손실 함수로는 평균 제곱 오차(Mean Squared Error, MSE)와 크로스 엔트로피 오차(Cross Entropy Error, CEE)가 있습니다.

평균 제곱 오차

실제 값과 예측 값의 차이(error)를 제곱하여 평균을 낸 것이 평균 제곱 오차(MSE)입니다. 실제 값과 예측 값의 차이가 클수록 평균 제곱 오차의 값도 커진다는 것은 반대로 생각하면 이 값이 작을수록 예측력이 좋다는 것을 의미합니다. 평균 제곱 오차는 회귀에서 손실 함수로 주로 사용됩니다.

다음은 평균 제곱 오차를 구하는 수식입니다.

텐서플로 2에서는 다음과 같이 사용합니다.

model.compile(optimizer=tf.keras.optimizers.SGD(lr=0.1), loss='mse')