학습으로 가우시안 혼합 모델의 모든 파라미터 π, μ, Σ의 값이 결정되었다면, 베이즈 정리(Bayes’ theorem)를 이용하여 γ(z_nk)를 다음과 같이 정리할 수 있습니다.

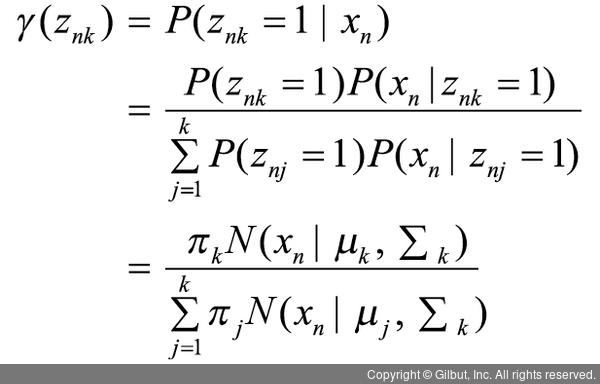
π_k와 p(z_nk=1)은 모두 K번째 가우시안 분포에 선택될 확률을 나타내기 때문에 수식에서 p(z_nj=1)이 π_j로 치환되었습니다.

π_k는 z_k=1일 때의 사전 확률 값이며, γ(z_nk)는 관찰 데이터 x가 주어졌을 때의 사후 확률 값입니다. 또한, γ(z_k)를 성분 K에 대한 책임 값(responsibility)이라고 합니다.

그럼 이제 코드로 확인해 보겠습니다.

사이킷런을 이용하여 GMM을 구현해 보겠습니다. 데이터셋은 data.npy 파일을 사용할 텐데, 이 파일은 배열 한 개를 넘파이 형식으로 저장해 놓은 것입니다.

먼저 필요한 라이브러리를 호출하고, 데이터를 메모리로 로딩합니다. 코드에서 사용된 data.npy 파일은 파이썬 소프트웨어 패키지가 만든 넘파이 배열 파일입니다.