11.2.3 자기 조직화 지도

자기 조직화 지도(Self-Organizing Map, SOM)는 신경 생리학적 시스템을 모델링한 것으로, 입력 패턴에 대해 정확한 정답을 주지 않고 스스로 학습을 하여 클러스터링(clustering)하는 알고리즘입니다.

SOM 구조

핀란드 헬싱키 공과 대학교의 테우보 코호넌(Teuvo Kohonen)은 자기 조직화 지도를 설명하려고 네트워크를 층 두 개로 구성했습니다. 입력층(input layer)과 2차원 격자(grid)로 된 경쟁층(competitive layer)인데, 입력층과 경쟁층은 서로 연결되어 있습니다. 이때 가중치는 연결 강도(weight)를 나타내며, 0과 1 사이의 정규화(normalize)된 값을 사용합니다.

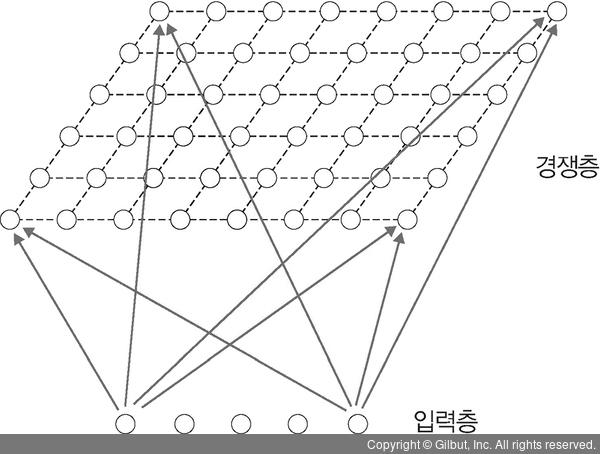
▲ 그림 11-13 자기 조직화 지도

자기 조직화 지도의 학습은 네 단계로 진행됩니다.

1. 초기화(initialization): 모든 연결 가중치는 작은 임의의 값으로 초기화합니다.

2. 경쟁(competition): 자기 조직화 지도는 경쟁 학습(competive learning)을 이용하여 입력층과 경쟁층을 연결합니다. 자기 조직화 지도는 연결 강도 벡터가 입력 벡터와 얼마나 가까운지 계산하여 가장 가까운 뉴런이 승리하는 ‘승자 독점(winner take all)’ 방식을 사용합니다. 이때 사용되는 수식은 다음과 같습니다.

D_ij 값이 작을수록 연결 강도 벡터와 입력 벡터가 가까운 노드이며, 연결 강도는 다음 식을 사용하여 새로운 값으로 업데이트합니다.

연결 강도 벡터와 입력 벡터가 가장 가까운 뉴런으로 계산되면 그 뉴런의 이웃 뉴런들도 학습을 하게 되는데, 이때 모든 뉴런이 아닌 제한된 이웃 뉴런들만 학습합니다.

3. 협력(cooperation): 승자 뉴런은 네트워크 토폴로지에서 가장 좋은 공간 위치를 차지하게 되며, 승자와 함께 학습할 이웃 크기를 정의합니다.

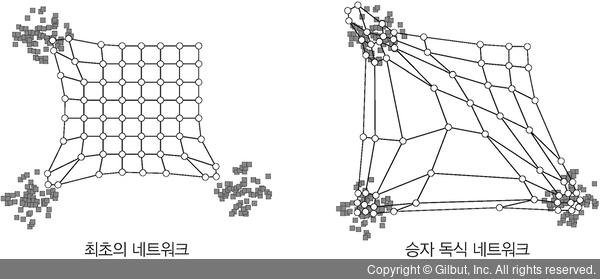
▲ 그림 11-14 최초의 네트워크와 승자 독식 네트워크

4. 적응(adaptation): 승리한 뉴런의 가중치와 이웃 뉴런을 업데이트합니다.

그리고 최종적으로 원하는 횟수만큼 2~3의 과정을 반복합니다.

자기 조직화 지도를 예제로 살펴보기

자기 조직화 지도를 구현해 볼 텐데, 데이터셋은 사이킷런에서 제공하는 숫자(digit) 필기 이미지를 사용합니다.

자기 조직화 지도를 위해 MiniSom 라이브러리를 설치합니다.

> pip install MiniSom

먼저 필요한 라이브러리를 호출하고 사이킷런에서 제공하는 숫자 필기 이미지 데이터셋을 내려받습니다.

코드 11-10 라이브러리 호출 및 데이터셋 내려받기

import numpy as np
from sklearn.datasets import load_digits
from minisom import MiniSom
from pylab import plot, axis, show, pcolor, colorbar, bone

digits = load_digits() ------ 숫자 필기 이미지 데이터셋 내려받기
data = digits.data ------ 훈련 데이터셋
labels = digits.target ------ 정답(레이블)

이제 클러스터링을 위해 MiniSom 알고리즘을 사용합니다. MiniSom 알고리즘을 생성하면서 지도에 대한 차원과 입력 데이터의 차원을 함께 정의합니다.

코드 11-11 훈련 데이터셋을 MiniSom 알고리즘에 적용

som = MiniSom(16, 16, 64, sigma=1.0, learning_rate=0.5) ------ ①
som.random_weights_init(data)
print("SOM 초기화.")
som.train_random(data,10000)
print("/n . SOM 진행 종료")

bone()
pcolor(som.distance_map().T)
colorbar()

① MiniSom은 시각화 기능이 거의 없는 SOM을 구현할 수 있는 라이브러리로, 여기에서 사용되는 파라미터는 다음과 같습니다.

다음 그림은 훈련 데이터셋을 MiniSom 알고리즘에 적용한 결과입니다.

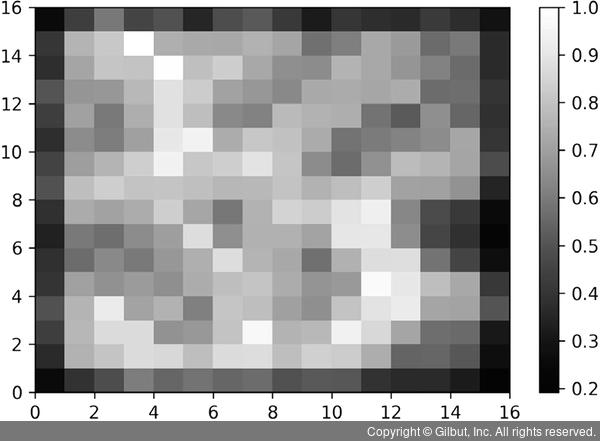
▲ 그림 11-15 훈련 데이터셋을 MiniSom 알고리즘에 적용한 결과

다음으로 각 클래스에 대해 레이블을 설정하고 색상을 할당한 후 시각화된 SOM에서 클래스를 구분합니다.

코드 11-12 클래스에 대해 레이블 설정 및 색상 할당

labels[labels=='0'] = 0 ------ 레이블 설정
labels[labels=='1'] = 1 -----|
labels[labels=='2'] = 2 -----|
labels[labels=='3'] = 3 -----|
labels[labels=='4'] = 4 -----|
labels[labels=='5'] = 5 -----|
labels[labels=='6'] = 6 -----|
labels[labels=='7'] = 7 -----|
labels[labels=='8'] = 8 -----|
labels[labels=='9'] = 9 -----|

markers = ['o', 'v', '1', '3', '8', 's', 'p', 'x', 'D', '*']
colors = ["r", "g", "b", "y", "c", (0,0.1,0.8), (1,0.5,0), (1,1,0.3), "m", (0.4,0.6,0)]
for cnt, xx in enumerate(data): ------ 시각화 처리
    w = som.winner(xx) ------ 승자(우승 노드) 식별
    plot(w[0]+.5, w[1]+.5, markers[labels[cnt]], ------ ①
         markerfacecolor='None', markeredgecolor=colors[labels[cnt]],
         markersize=12, markeredgewidth=2)
show()

① BMU(Best Matching Unit)를 이용하여 승자를 식별하고 클래스별로 마커를 플로팅합니다. 여기에서 BMU는 MiniSom 알고리즘을 이용해서 모든 가중치 벡터의 데이터 공간에서 유클리드 거리를 측정하여 승자를 식별합니다.

다음 그림은 클래스에 대해 레이블 설정 및 색상 할당 결과입니다.

▲ 그림 11-16 예제 실행 결과에 레이블과 색상 할당

이 코드는 16×16 노드로 구성된 플롯을 제공합니다. 중첩이 있기는 하지만, 대부분의 경우 각 클래스는 별도 영역을 차지하며 잘 분리되어 있는 것을 확인할 수 있습니다.