마르코프 체인은 시간에 따른 상태 변화를 나타내며, 이때 상태 변화를 전이(transition)라고 합니다. 마르코프 프로세스에서 상태 간 이동인 전이는 확률로 표현하게 되는데, 이를 상태 전이 확률(state transition probability)이라고 합니다. 즉, 시간 t에서의 상태를 s라고 하며, 시간 t+1에서의 상태를 s'라고 할 때 상태 전이 확률은 다음과 같이 수식으로 표현할 수 있습니다.

상태 전이 확률은 어떤 상태 i가 있을 때 그다음 상태 j가 될 확률을 의미합니다. 여기에서 P(A|B)는 조건부 확률로 B가 발생했을 때 A가 발생할 확률을 의미합니다.

예를 들어 다음 그림은 병원을 방문한 어느 하루에 대한 마르코프 체인을 표현한 것입니다. 이 날의 상태가 병원에서의 대기와 진찰, 독서, 웹 서핑, 취침으로만 구성되어 있다고 가정하면, 다섯 가지 상태가 있는 마르코프 프로세스로 표현할 수 있습니다. 이때 하나의 상태에서 다른 상태로 이동할 확률의 합은 1을 유지한 상태로, 여러 상태가 연쇄적으로 이어져 있습니다. 예를 들어 대기 → 진찰, 대기 → 독서, 대기 → 웹 서핑으로 진행되는 모든 프로세스의 합은 1이 되어야 합니다. 또한, ‘취침’은 하루를 끝마치는 종료 상태에 해당됩니다.

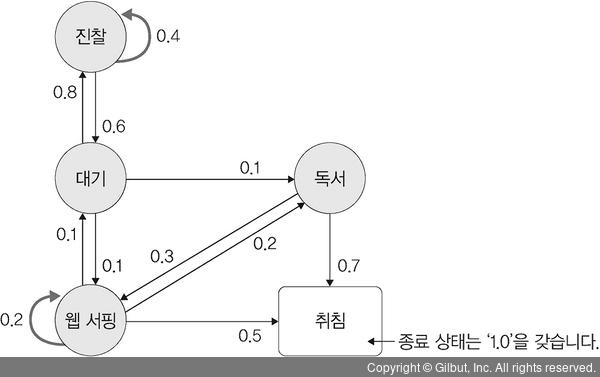
▲ 그림 12-2 마르코프 프로세스 사례